问题描述
给定平面上 $n$ 个点的集合 $Q$,$Q$ 的凸包是一个凸多边形 $P$。$Q$ 的点或者在 $P$ 上或者在 $P$ 内,并且连接 $P$ 内任意两点的边都在 $P$ 内。现在要求 $Q$ 的凸包 $P$。
问题分析
Graham-scan 的基本思想:
- 找到最下最左顶点,其他顶点与它连线。
- 按夹角从小到大排序。
- 夹角最小的开始,寻找凸包点。

是否存在分治的方法?
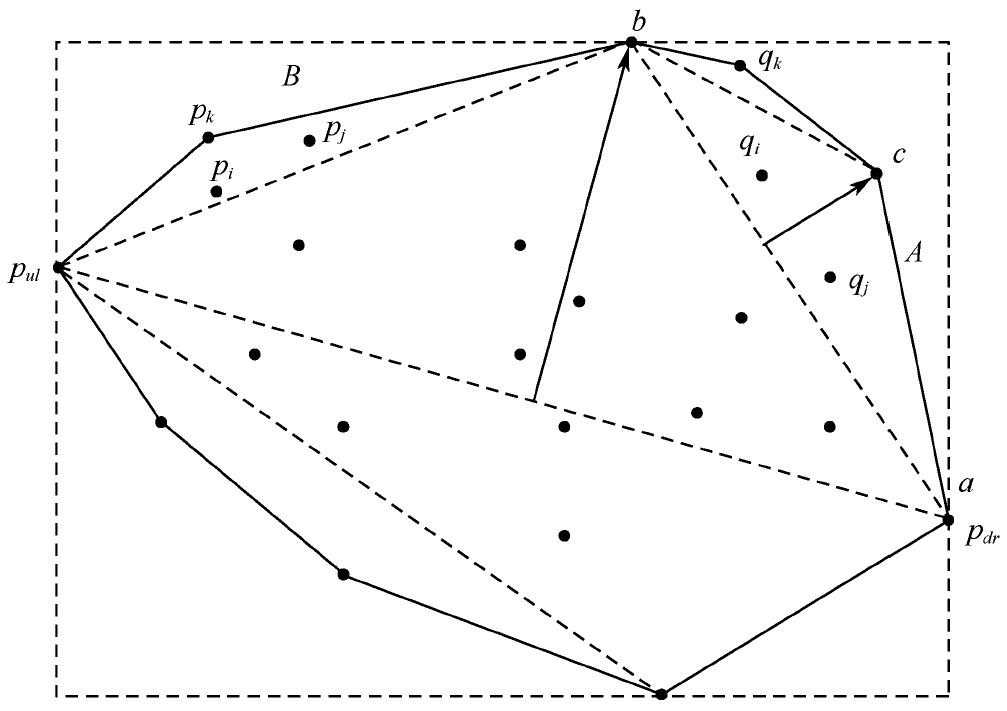
- 取两极端点,最右最下点 $p_{dr}$ 和最左最上点 $p_{ul}$。
- 有向线 $p_{dr}p_{ul}$ 将整个凸包被划分为右凸包和左凸包。
- 对右凸包和左凸包分别进行递归。
算法分析
- 时间复杂度:$O(n \log {n})$