问题描述
找任意起点到任意终点的一条最短路径。
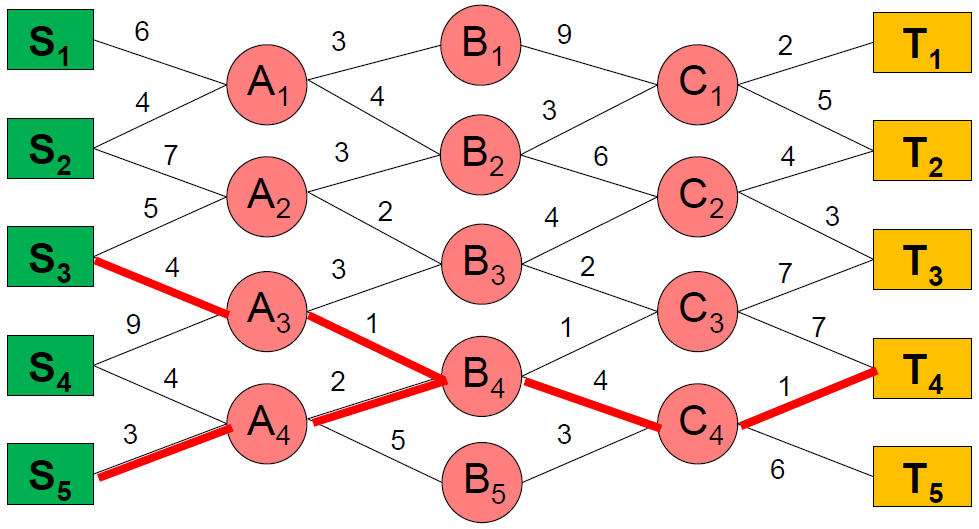
形式化定义
输入:
- 起点集合 $\{S_1, S_2, \cdots, S_n\}$
- 终点集合 $\{T_1, T_2, \cdots, T_m\}$
- 中间结点集合,边集
输出:
- 一条从起点到终点的最短路径
问题分析
蛮力法的时间复杂度为 $O(2^n)$。因此采用动态规划方法。
动态规划求解多级图问题是一个多阶段决策过程。每一步求解的问题是后面阶段求解问题的子问题,每步决策将依赖于以前步骤的决策结果。

优化原则
优化函数的特点:任何最短路的子路径相对于子问题始、终点最短。
优化原则:一个最优决策序列的任何子序列本身一定是相对于子序列的初始和结束状态的最优决策序列。
反例

本题要求总长模 $10$ 的最小路径。动态规划算法的解为:DUUU,而最优解其实是 DDDD。
这是因为不满足优化原则,不能用动态规划的方法!