连通分量
若图中的若干顶点之间两两可达,那么称这些顶点之间是连通的。
无向图的极大连通子图,称为连通分量。
深度优先搜索
可以采用 DFS 的方法快速找到无向图中的连通分量。具体做法是,只要图中有顶点没有被访问过,那么就从中选择一个顶点开始进行 DFS,DFS 完成后将当前所有遍历过的顶点组成的子图视为一个连通分量。如此下去,直到图中所有顶点均访问完毕。
算法代码
辅助空间定义
vector<bool> marked(G.numV);
vector<int> id(G.numV);
int count = 0;
借助深度优先搜索
void DFS(Graph G, int v) {
marked[v] = true;
id[v] = count;
for (auto w : G.adj[v]) {
if (!marked[w]) {
DFS(G, w);
}
}
}
求解无向图的强连通分量
void CC(Graph G) {
for (int v = 0; v < G.numV; ++v) {
if (!marked[v]) {
DFS(G, v);
++count;
}
}
}
bool connected(int v, int w) {
return id[v] == id[w];
}
强连通分量
如果同时存在从 v 到 w 的有向路径和从 w 到 v 的有向路径,则顶点 v 和 w 是强连通的。
若有向图中的若干顶点之间两两可达,那么称这些顶点之间是强连通的。若将有向图转化成无向图后,这些顶点是连通的,那么称这些顶点之间是弱连通的。
有向图的极大强连通子图,称为强连通分量。有向图转化为无向图后,若出现了新的连通分量,称为弱连通分量。
Kosaraju-Sharir 算法
Kosaraju-Sharir 算法是一种可以在线性时间内找到有向图强连通分量的算法,需要用到拓扑排序的相关知识。
算法首先需要构造图 $G$ 的反向图 $G^R$。显然,$G$ 和 $G^R$ 的强连通分量是完全相同的。
Kosaraju-Sharir 算法接下来需要将每个顶点视为单个强连通分量以完成初始化,然后在每个强连通分量内进行拓扑排序。具体来说,算法分为如下两步:
- 计算 $G^R$ 的反向后序。
- 在 $G$ 中运行 DFS,以 $G^R$ 的反向后序访问未标记的顶点。
算法代码
辅助空间定义
vector<bool> marked(G.numV);
vector<int> id(G.numV);
int count = 0;
借助深度优先搜索
void DFS(DiGraph G, int v) {
marked[v] = true;
id[v] = count;
for (auto w : G.adj[v]) {
if (!marked[w]) {
DFS(G, w);
}
}
}
求解无向图的强连通分量
void KosarajuSharirSCC(DiGraph G) {
for (int v : G.reverse().topo_sort()) {
if (!marked[v]) {
DFS(G, v);
++count;
}
}
}
bool connected(int v, int w) {
return id[v] == id[w];
}
算法分析
时间复杂度:$O(E + V)$
Tarjan 算法
Tarjan 算法是一种由 Robert Tarjan 提出的求解有向图强连通分量的算法,它能做到线性时间的复杂度。
在 Tarjan 算法中,有如下定义:
DFN[i]:在 DFS 中该节点被搜索的次序(时间戳),换而言之就是第几个被搜索到。LOW[i]:为i或i的子树能够追溯到的最早的栈中节点的次序号。- 当
DFN[i] == LOW[i]时,i或i的子树可以构成一个强连通分量。
算法自然语言描述
首先初始化一个空的栈。每次访问一个新节点(该节点入栈),如果这个点出度不为零就继续往下找,直到找到底。每次回溯时都取子节点与这个节点的 LOW 值的最小值,保证最小的子树根。如果找到 DFN == LOW 就说明这个节点是这个强连通分量的根节点(毕竟这个 LOW 值是这个强连通分量里最小的)。最后找到强连通分量的节点后,就将这个栈里,比此节点后进来的节点全部出栈,它们就组成一个全新的强连通分量。
下面来举一个具体的例子说明 Tarjan 算法的执行流程。

如图所示的有向图中包含 3 个强连通分量,分别为 ${1, 2, 4, 5}$、${3}$ 和 ${6}$。

首先访问节点 $1$,之后陆续访问节点 $2$、$3$、$6$,DFN 的值和 LOW 值都相同(等于被搜索的次序)。
现在发现节点 $6$ 没有后继,因此需要进行回溯。回溯第一步发现 DFN[6] == LOW[6],因此 ${6}$ 为强连通分量,出栈。同理,DFN[3] == LOW[3],因此 ${3}$ 也为强连通分量,出栈。
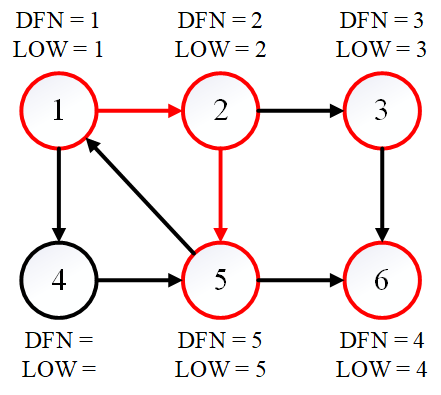
现在回溯到节点 $2$,发现它有后继节点 $5$,继续搜索。然而节点 $5$ 的后继都已经被访问过了,因此节点 $5$ 的 LOW 值需要更新,LOW[5] = 5,DFN[1] = 1 而 DFN[4] = 4,因此 LOW[5] = 1。
下面仍然回溯到节点 $2$。由于节点 $5$ 已经被访问过了,节点 $2$ 的 LOW 值同样也需要更新。于是 LOW[2] = 1。
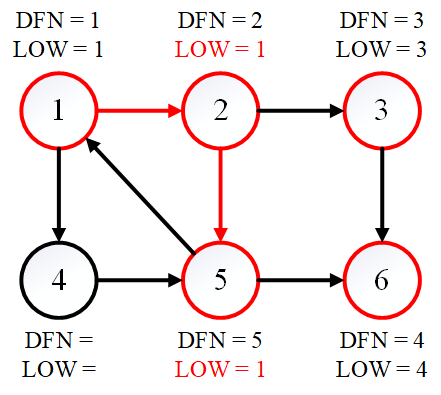
接下来回溯到节点 $1$,发现它有后继节点 $4$,继续搜索。然而节点 $4$ 的后继都已经被访问过了,因此节点 $4$ 的 LOW 值需要更新,LOW[4] = 5。
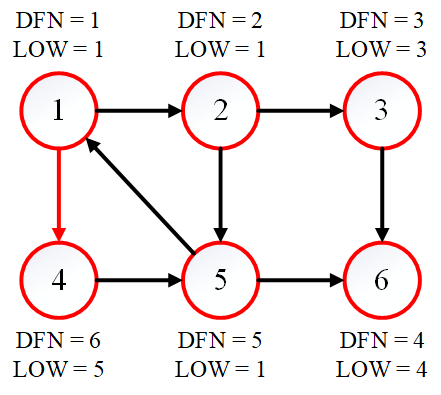
最后再次回溯到节点 $1$,此时所有的节点都已访问,并且 DFN[1] == LOW[1]。因此节点 $1$ 及其后续所有节点全部出栈,${1, 2, 4, 5}$ 为强连通分量。
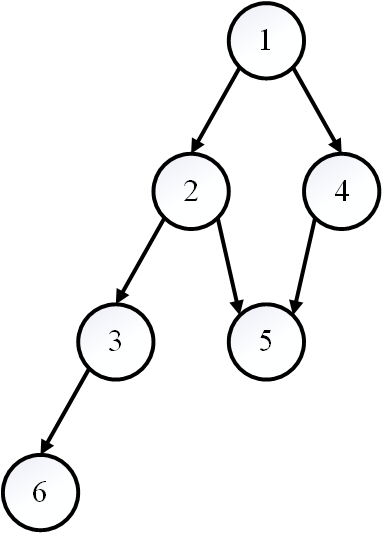
整个算法的 DFS 搜索树如图所示。