流网络
设 $G=(V, E)$ 是一个有向图,其中每条边 $(u, v)$ 有一个非负的容量值 $c(u, v)$。如果 $E$ 中包含一条边 $(u,v)$,那么图中就不存在它的反向边。而且,$G$ 中有且只有一个入度为零的节点 $s$ 和出度为零的节点 $t$,它们分别被称为源点和汇点。称这样的有向图 $G$ 为流网络。
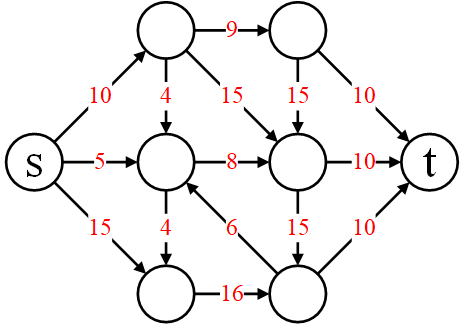
在流网络中,边的含义不再是有向图中的权重,而是容量 $c(u, v)$。实际流过节点的网络流的流量 $f(u, v)$ 需要满足如下条件:
- 容量限制:$0 \geqslant f(u, v) \geqslant c(u, v)$
- 流量守恒:$\sum_{u \in V} f(u, v)= \sum_{v \in V} f(u, v)$
简单应用
流网络常见的一种应用场景是运输问题,需要将货物从 $s$ 运输到 $t$,途经几个中转站,每次运输到每个中转站的货物的数量是有限制的。在实际应用中我们可能会在某条边上双向运输,这样便违反了我们之前对流网络的定义,但是我们可以将包含反平行边的图来改造成流网络,具体的方法是引入一个是虚构的中转结点,方法如下图。

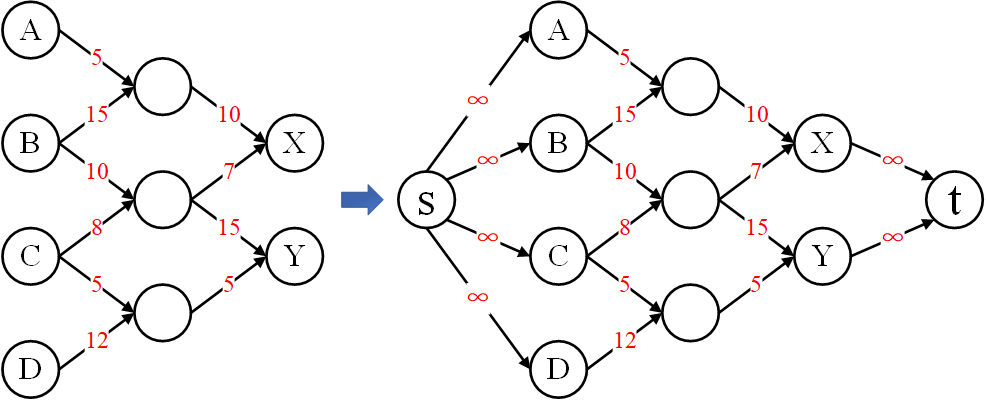
考虑另外一种特殊情形,从多个工厂发出货物最终运输到别的多个工厂,这时候我们具有了多个源点和多个汇点,这也很好解决,解决的方法就是人为添加超级源点 supersource 和超级汇点 supersink,具体方法见下图。
最大流
如图所示,绿色的值表示流网络中的实际流量大小,它不能够超过每条边上的容量值。
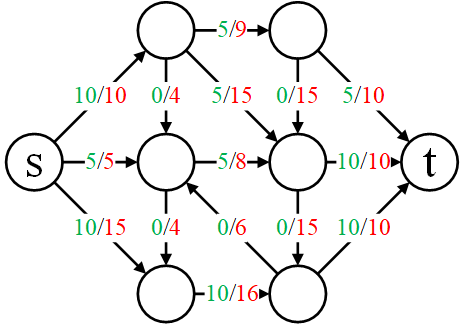
现在的问题是,整个网络存在比上图中更大的流量吗?如果有,如何求解?
Ford-Fulkerson 算法
Ford-Fulkerson 算法是求解流网络中的最大流的算法,其核心是通过引入残存网络 residual network 和增广路径 augmenting path 的概念对原先的运输方案进行纠错、改进。
最小割
TODO
最大二部图匹配
在二部图中选择尽可能多的边,并且任意两条边不共享同一节点,这就是最大二部图匹配问题。
例如,有 $M$ 个求职者和 $N$ 个职位。每个求职者都有他感兴趣的工作子集。每个职位空缺只能接受一个求职者,一个求职者只能被任命为一个职位。为申请人找到工作分配,以便尽可能多的申请人获得工作。
最大二部图匹配问题最终可以转化成最大流-最小割问题进行求解。
TODO