问题描述
从图中的某个顶点出发到达另外一个顶点的所经过的边的权重和最小的一条路径,称为最短路径。
单源最短路径:Dijkstra 算法
Dijkstra 算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题,算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。
算法自然语言描述
Dijkstra 算法基于广度优先搜索算法,在遍历图的过程中更新从起点到目标节点的最短路径。算法需要用到两个数组 dist 和 visit,分别表示最短路径和是否被访问过。为了实现广度优先搜索,还需要使用一个队列。起点的 dist 被初始化为 $0$,visit 被初始化为布尔值 true,然后进入队列中。其他节点的 dist 被初始化为 $\infty$,visit 被初始化为布尔值 false。
每次搜索时弹出队首节点,寻找其直接后继。在寻找直接后继的过程中,如果未访问过该节点则更新最短路径;如果访问过该节点,则需要判断如果从该节点经过到其他节点的路径是否更短,如果更短则更新到其他节点的最短路径。这个过程有一个非常形象的说法叫做边的松弛。
下面举一个具体的例子详细说明:

如图所示,以 $A$ 为起点,dist[0] = 0,visit[0] = 1,然后节点 $A$ 进入队列中。
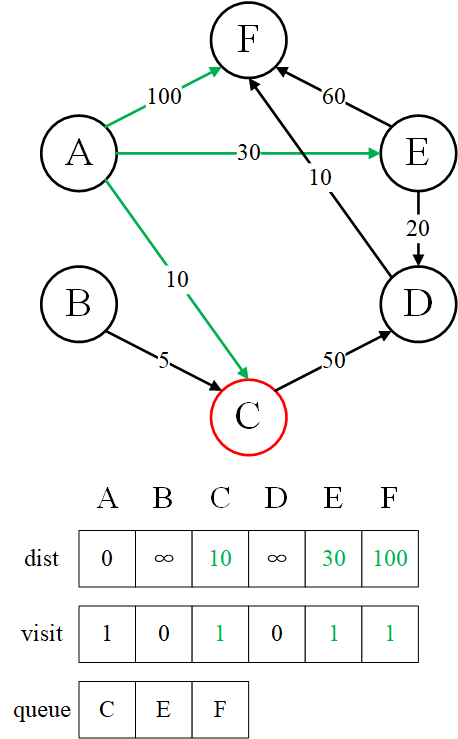
接下来队首节点 $A$ 出队,它有 3 个直接后继 $C$、$E$、$F$,节点 $A$ 到这些节点的最短路径即为 3 条边上的权重。

接下来队首节点 $C$ 出队,它有 1 个直接后继 $D$。节点 $A$ 到节点 $D$ 的最短路径本来为 $\infty$,经过节点 $C$ 周转之后路径更短,更新为 $60$。
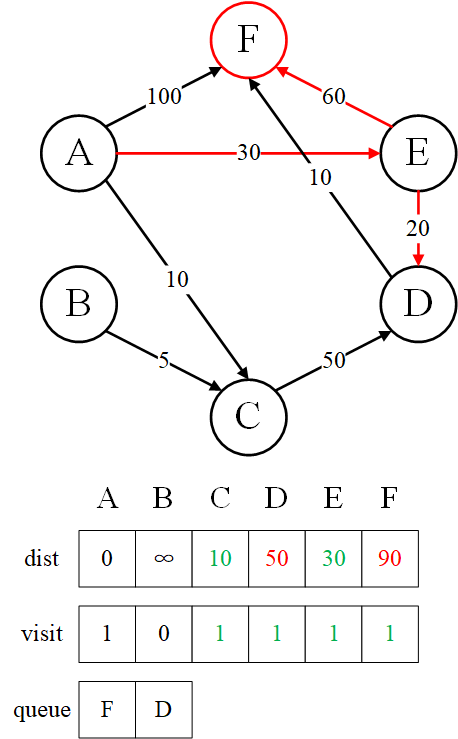
接下来队首节点 $E$ 出队,它有 2 个直接后继 $D$ 和 $F$。节点 $A$ 到节点 $D$ 的最短路径本来为 $60$,经过节点 $E$ 周转之后路径更短,更新为 $50$。同理,节点 $A$ 到节点 $F$ 的最短路径本来为 $100$,经过节点 $E$ 周转之后路径更短,为 $90$。

接下来队首节点 $F$ 出队,它有没有直接后继。

接下来队首节点 $D$ 出队,它有 1 个直接后继 $F$。节点 $A$ 到节点 $F$ 的最短路径本来为 $90$,经过节点 $D$ 周转之后路径更短,更新为 $60$。
多源最短路径
给定一个有向图和一组源顶点,找到从集合中的任意顶点到其他顶点的最短路径。
实现多源最短路径算法,只需要使用 BFS,但算法一开始需要将所有源顶点入队进行初始化。
一个典型例子是网络爬虫。如果要从一个网页上爬取一些相关的连接,应该用 DFS 还是 BFS?
答案显然是 BFS。因为一个网页上可能有多个网址,点开这些网址以后打开的新的网页又会有其他一些新的网址……如果采用 DFS,很可能在找第一个网址的时候就非常深入了,难以回溯。而且网络爬虫非常符合多源最短路径的场景,因为一个网页上面有多个网址(入口)。
算法进阶
如何对边进行“松弛”?
针对不同类型权重的边,需要采用合适的算法来进行“松弛”:
- 非负权重:Dijkstra 算法
- 无有向循环:拓扑排序算法
- 无负循环:Bellman-Ford 算法
最长路径(关键路径)
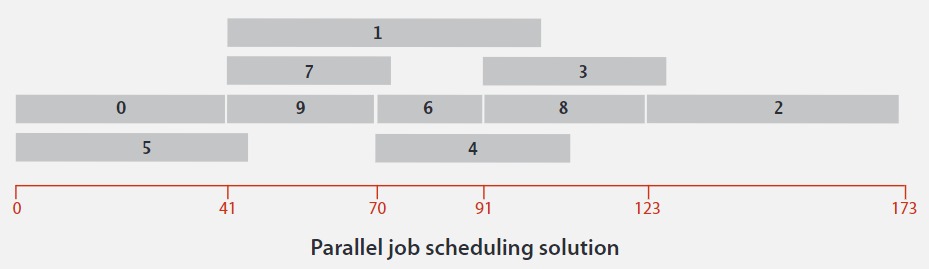
应用场景:并行作业调度。给定一组具有持续时间和优先级约束的作业,安排作业(通过为每个作业找到开始时间)以达到最短完成时间,同时尊重约束。

要解决并行作业调度问题,需要创建边加权 DAG。
- 源和汇顶点
- 每个作业的两个顶点(开始和结束)
- 每个作业的三个边
- 开始到结束(按持续时间加权)
- 源开始(0 权重)
- 端到下沉(0 权重)
- 每个优先约束的一条边(0 权重)
负权重边
Dijkstra 算法无法处理负权重边。
通过转化的方法将边权重置为非负,Dijkstra 算法仍不适用。
负环
若出现负环,我们几乎很难判断是否有最短路径的存在。
但是如果只是有环,而非负环,是可以找到最短路径的。
Bellman-Ford 算法
for (int i = 0; i < G.numV; ++i) {
for (int v = 0; v < G.numV; ++v) {
for (DirectedEdge &e : G.adj[v]) {
relax(e);
}
}
}
边的“松弛”
void relax(DirectedEdge e) {
int v = e.from(), w = e.to();
if (distTo[w] > distTo[v] + e.weight()) {
distTo[w] = distTo[v] + e.weight();
edgeTo[w] = e;
}
}
小结
| 算法 | 条件 | 时间复杂度 | 空间复杂度 |
|---|---|---|---|
| 拓扑排序 | 无有向环 | $E+V$ | $V$ |
| Dijkstra | 权重非负 | $E \log V$ | $V$ |
| Bellman-Ford | 无负环 | $EV$ | $V$ |