定义
如果 $\operatorname{dom} f$ 是凸集,且对于任意的 $x, y \in \operatorname{dom} f$ 和任意的 $0 \leqslant \theta \leqslant 1$,若有
$$ f(\theta x+(1-\theta) y) \leqslant \theta f(x)+(1-\theta) f(y) $$则称函数 $f: \mathbf{R}^n \rightarrow \mathbf{R}$ 是凸的。
从几何意义上看,上述不等式意味着点 $(x, f(x))$ 和点 $(y, f(y))$ 之间的线段,即从 $x$ 到 $y$ 的弦,在函数 $f$ 图像的上方。如果不等式中当 $x \ne y$ 时 $0 \leqslant \theta \leqslant 1$ 严格成立,则称函数 $f$ 是严格凸的。
扩展值延伸
通常可以定义凸函数的定义域外的值为 $\infty$,从而将这个凸函数延伸至全空间 $\mathbf{R}^n$。我们定义凸函数 $f$ 的扩展值延伸:$\tilde{f}: \mathbf{R}^n \rightarrow \mathbf{R} \cup {\infty}$ 如下:
$$ \tilde{f}(x)=\left\{\begin{array}{ll} f(x) & x \in \operatorname{dom} f \\ \infty & x \notin \operatorname{dom} f \end{array}\right. $$一阶条件
假设 $f$ 可微(即其梯度 $\nabla f$ 在开集 $\operatorname{dom} f$ 内处处存在),则函数 $f$ 是凸函数的充要条件是 $\operatorname{dom} f$ 是凸集,且对于任意的 $x, y \in \operatorname{dom} f$,有
$$ f(y) \geqslant f(x)+\nabla f(x)^{\top}(y-x) $$由此得出的仿射函数 $y$ 即为函数 $f$ 在点 $x$ 附近的 Taylor 近似。上面的不等式表明,对于一个凸函数,其一阶 Taylor 近似实质上是原函数的一个全局下估计。反之,如果某个函数的一阶 Taylor 近似总是其全局下估计,那么这个函数是凸的。
同理,可以定义凹函数及其一阶条件。
二阶条件
现在假设函数 $f$ 二阶可微(即对于开集 $\operatorname{dom} f$ 内的任意一点,它的 Hessian 矩阵或者二阶导数 $\nabla ^2 f$ 存在),则函数 $f$ 是凸函数的充要条件是,其 Hessian 矩阵是半正定矩阵,即对所有的 $x \in \operatorname{dom} f$,有
$$ \nabla ^2 f(x) \succeq 0 $$下水平集
函数 $f: \mathbf{R}^n \rightarrow \mathbf{R}$ 的 α-下水平集定义为
$$ C_\alpha = \{ x \in \operatorname{dom} f \mid f(x) \leqslant \alpha \} $$上境图
函数 $f: \mathbf{R}^n \rightarrow \mathbf{R}$ 的图像定义为
$$ \{ (x, f(x)) \mid x \in \operatorname{dom} f \} $$它是 $\mathbf{R}^{n+1}$ 空间的一个子集。
函数 $f: \mathbf{R}^n \rightarrow \mathbf{R}$ 的上镜图定义为
$$ \operatorname{epi} f = \{ (x, f(x)) \mid x \in \operatorname{dom} f, f(x) \leqslant t \} $$上镜图的概念很像是下水平集和函数图像二者的结合。从几何上看,上镜图即为在函数图像之上。
定义在 $\mathbf{R}^n$ 上的凸函数 $f$ 的上镜图是 $\mathbf{R}^{n+1}$ 空间的一个凸集,其支撑超平面和一阶条件有着如下图所示的联系:
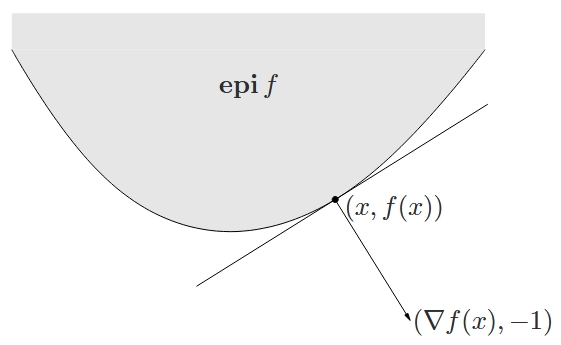
从图中可以直观地看到,凸函数 $f$ 在点 $x$ 处的一阶 Taylor 近似即为其上镜图在 $x$ 处的支撑超平面。
Jensen 不等式及其扩展
基本不等式
$$ f(\theta x+(1-\theta) y) \leqslant \theta f(x)+(1-\theta) f(y) $$有时也称作 Jensen 不等式。此不等式可以很方便地扩展至更多点的凸组合:如果函数 $f$ 是凸函数,$x_1, \cdots, x_k \in \operatorname{f}$,$\theta_1, \cdot, \theta_k \geqslant 0$ 且 $\theta_1 + \cdots + \theta_k = 1$,则下式成立
$$ f(\theta_1 x_1 + \cdots + \theta_k x_k) \leqslant \theta_1 f(x_1) + \cdots + \theta_k f(x_k) $$考虑凸集时,此不等式还可以扩展至无穷项和、积分以及期望。
例如,若在 $S \subseteq \operatorname{dom} f$ 上 $p(x) \geqslant 0$ 且 $\int_{S} p(x) \mathrm{d} x = 1$,则
$$ f\left(\int_{S} p(x) x \mathrm{~d} x\right) \leqslant \int_{S} f(x) p(x) \mathrm{d} x $$再比如,设 $x$ 是随机变量,若函数 $f$ 是凸函数,则
$$ f(\mathbf{E}x) \leqslant \mathbf{E} f(x) $$我们不妨来回忆以下高中时期我们接触到的凸函数定义,如下
$$ f\left(\frac{x+y}{2}\right) \leqslant \frac{f(x)+f(y)}{2} $$
其实这就是由 Jensen 提出的最初的一个最简单的不等式。现在,我们可以称上述所有的不等式为 Jensen 不等式。