定义
当凸优化问题的目标函数是凸二次型并且约束函数为仿射时,该问题被称为二次规划(Quadratic Program, QP)。二次规划问题可以表示为
$$ \begin{aligned} \mathrm{minimize} \quad & \frac{1}{2} x^{\top}Px + q^{\top}x + r \\ \mathrm{subject\ to} \quad & Gx \preceq h \\ \quad & Ax = b \end{aligned} $$其中 $P \in \mathbf{S}^n_+$,$G \in \mathbf{R}^{p \times n}$。可以用下图来表示二次规划问题。
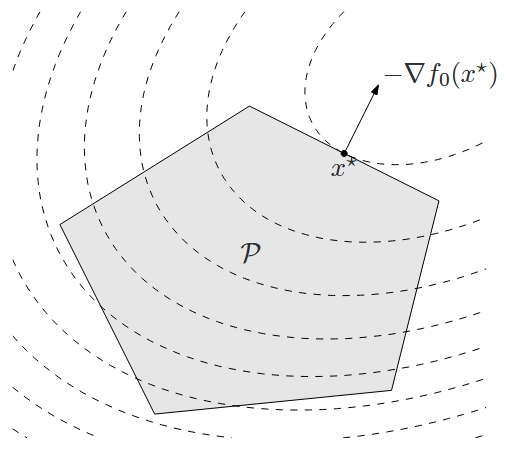
二次约束二次规划
如果不仅是目标函数,而且不等式约束也是凸二次型,即
$$ \begin{aligned} \mathrm{minimize} \quad & \frac{1}{2} x^{\top}Px + q^{\top}x + r \\ \mathrm{subject\ to} \quad & \frac{1}{2} x^{\top}P_ix + q^{\top}_ix + r_i \leqslant 0 \\ \quad & Ax = b \end{aligned} $$则称这一问题为二次约束二次规划(Quadratically Constrained Quadratic Program, QCQP)
线性规划是二次规划的特例,即取 $P = 0$。二次规划是二次约束二次规划的特例,令 $P_i = 0$ 即可。
举例
最小二乘及回归
$$ \| Ax - b \|^2_2 = x^{\top}A^{\top}Ax - 2b^{\top}Ax + b^{\top}b $$上面的凸二次函数是一个(无约束的)二次规划。我们在很多领域都会看到类似的式子,有些地方会称其为回归分析或者最小二乘逼近。这个问题很简单,可以求出其解析解 $x = A^{\dagger} b$。
二阶锥规划
$$ \begin{aligned} \mathrm{minimize} \quad & f^{\top}x \\ \mathrm{subject\ to} \quad & \| A_ix + b_i \|_2 \leqslant c_i^{\top}x + d_i, \quad i = 1,\cdots,m \\ \quad & Fx = g \end{aligned} $$称上述问题为二阶锥规划(Second-Order Cone Program, SOCP),其中 $x \in \mathbf{R}^n$ 是优化变量,$A_i \in \mathbf{R}^{n_i \times n}$,$F \in \mathbf{R}^{p \times n}$。并且我们称约束
$$ \| Ax + b \|_2 \leqslant c^{\top}x + d $$为二阶锥约束。
当 $c_i = 0$ 时,SOCP 等同于 QCQP。当 $A_i = 0$ 时,SOCP 退化为(一般的)线性规划。