对偶锥
若 $K$ 为一个锥,则集合
$$ \begin{align*} K^{*} = \{y \mid x^{\top} y \geqslant 0, \forall x \in K\} \end{align*} $$称为 $K$ 的对偶锥。从几何上看,对偶锥 $K^{*}$ 是与锥 $K$ 内的所有向量夹角不超过 $90$ 度的所有向量组成的集合。如图所示,以 $y$ 为法向量的半空间包含锥 $K$,因此 $y \in K^{*}$;而以 $z$ 为法向量的半空间不包含锥 $K$,因此 $z \notin K^{*}$。
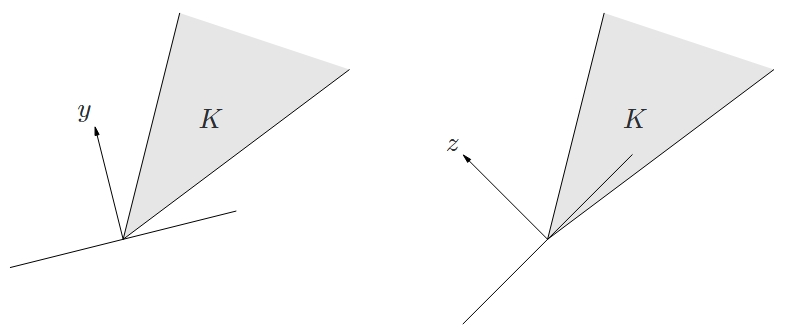
对偶锥的性质
- $K^{*}$ 是闭凸锥。
- $K_1 \subseteq K_2 \Rightarrow K_2^{*} \subseteq K_1^{*}$。
- 如果 $K$ 有非空内部,那么 $K^{*}$ 是尖的。
- 如果 $K$ 的闭包是尖的,那么 $K^{*}$ 有非空内部。
- $K^{**}$ 是 $K$ 的凸包的闭包。因此如果 $K$ 是凸和闭的,那么 $K^{**}=K$。
广义不等式的对偶
若凸锥 $K$ 是正常锥,则其对偶锥 $K^{*}$ 也是正常锥,它可以导出一个广义不等式 $\preceq_{K^{*}}$。
广义不等式及其对偶的性质
$$ \begin{align*} x \preceq_K y \Leftrightarrow \forall \lambda \succeq _{K^{*}} 0, \lambda^{\top} x \leqslant \lambda^{\top} y \\ x \prec_K y \Leftrightarrow \forall \lambda \succeq _{K^{*}} 0 \wedge \lambda \ne 0, \lambda^{\top} x < \lambda^{\top} y \end{align*} $$对偶不等式定义的最(极)大(小)元
最小元的对偶性质
$x$ 是 $S$ 上关于广义不等式 $\preceq_K$ 的最小元的充要条件是,对于 $\forall \lambda \succ_{K^{*}} 0$,$x$ 是在 $z \in S$ 上极小化 $\lambda^{\top} z$ 的唯一最优解。从几何上看,这意味着对于 $\forall \lambda \succ_{K^{*}} 0$,超平面 ${z \mid \lambda^{\top} (z-x) = 0}$ 是在 $x$ 处对 $S$ 的一个严格支撑超平面。如图所示。
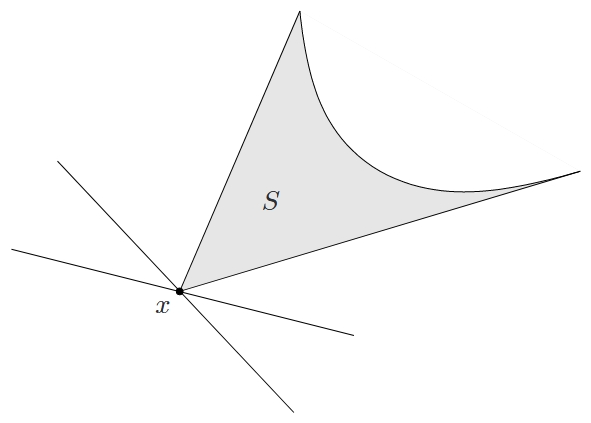
极小元的对偶性质
如果 $\lambda \succ _{K^{*}} 0$ 并且 $x$ 在 $z \in S$ 上极小化 $\lambda^{\top} z$,那么 $x$ 是极小的,如图所示。
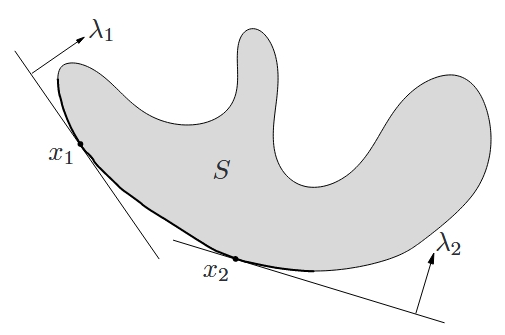
其逆命题在一般情况下是不成立的。