通过函数值集合理解强弱对偶性
可以通过集合
$$ \begin{aligned} \mathcal{G}=\{(f_1(x), &\cdots, f_m(x), \\ h_1(x), &\cdots, h_p(x), f_0(x)) \in \mathbf{R}^m \times \mathbf{R}^p \times \mathbf{R} \mid x \in \mathcal{D}\} \end{aligned} $$给出对偶函数的简单几何解释。事实上,此集合是约束函数和目标函数所取得的函数值。利用集合 $\mathcal{G}$,可以很容易地表达优化问题的最优值 $p^{\star}$。
$$ p^{\star} = \inf \{ t \mid (u, v, t) \in \mathcal{G}, u \preceq 0, v = 0 \} $$求解以 $(\lambda, \nu)$ 为自变量的对偶函数,得到
$$ g(\lambda, \nu) = \inf \{ (\lambda, \nu, 1)^{\top}(u, v, t) \mid (u, v, t) \in \mathcal{G} \} $$如果下确界有界,则不等式
$$ (\lambda, \nu, 1)^{\top}(u, v, t) \geqslant g(\lambda, \nu) $$定义了集合 $\mathcal{G}$ 的一个支撑超平面。
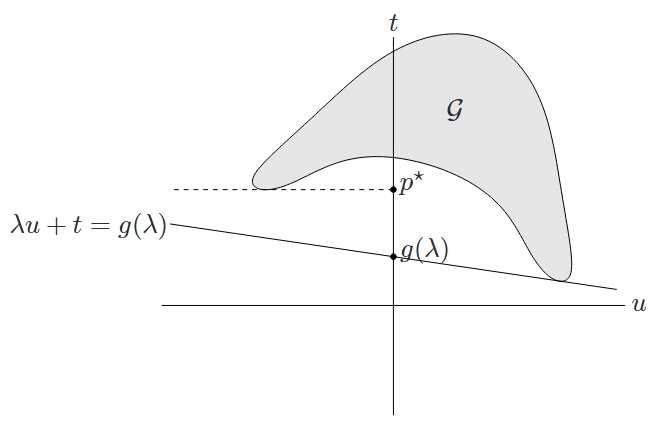
针对只有一个(不等式)约束的简单问题,对偶函数和下界 $g(\lambda) \leqslant p^{\star}$ 的几何解释如图所示。给定 $\lambda$,在集合 $\mathcal{G} = { (f_1(x), f_0(x)) \mid x \in \mathcal{D} }$ 上极小化 $(\lambda, 1)^{\top}(u, t)$,得到斜率为 $-\lambda$ 的支撑超平面。支撑超平面与坐标轴 $u = 0$ 的交点即为 $g(\lambda)$。
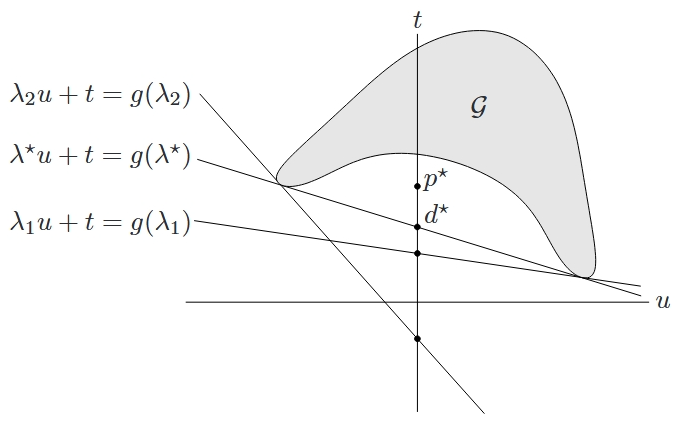
如图所示,对偶可行的三个 $\lambda$ 值对应的支撑超平面,这三个值中包含最优值 $\lambda^{\star}$。强对偶性此时不成立,最优对偶间隙 $p^{\star} - d^{\star} > 0$。
上镜图变化
通过下面的理解,我们就可以解释为什么对(大部分)凸问题,强对偶性总是成立。定义集合 $\mathcal{A} \subseteq \mathbf{R}^m \times \mathbf{R}^p \times \mathbf{R}$ 为
$$ \begin{aligned} \mathcal{A} &= G + \{ \mathbf{R}^M_+ \times \{ 0 \} \times \mathbf{R}_+ \} \\ &= \{ (u, v, t) \mid \exists x \in \mathcal{D}, f_i(x) \leqslant u_i, i=1,\cdots,m, \\ & \qquad h_i(x) = v_i, i=1,\cdots,p, f_0(x) \leqslant t \} \end{aligned} $$我们可以认为 $\mathcal{A}$ 是 $\mathcal{G}$ 的一种上镜图形式,因为 $\mathcal{A}$ 包含了 $\mathcal{G}$ 中的所有点以及一些“较坏”的点,即目标函数值或者不等式约束函数值较大的点。
可以用 $\mathcal{A}$ 来描述最优值
$$ p^{\star}=\inf \{t \mid (0,0,t) \in \mathcal{A}\} $$同样的,我们可以通过极小化仿射函数得到关于 $(\lambda, \nu)$ 的对偶函数
$$ g(\lambda, \nu)=\inf \{(\lambda, \nu, 1)^{\top}(u, v, t) \mid(u, v, t) \in \mathcal{A}\} $$如果确定下确界有界,则
$$ (\lambda, \nu, 1)^{\top}(u, v, t) \geqslant g(\lambda, \nu) $$定义了 $\mathcal{A}$ 的一个非竖直的支撑超平面。
特别地,由于 $(0, 0, p^{\star}) \in \operatorname{bd} \mathcal{A}$,我们有
$$ p^{\star} = (\lambda, \nu, 1)^{\top} (0, 0, p^{\star}) \geqslant g(\lambda, \nu) $$即弱对偶性成立。强对偶性成立,当且仅当存在某些对偶可行变量 $(\lambda, \nu)$,使得上式中的不等号取等号。从几何上看,对于集合 $\mathcal{A}$,存在一个边界点 $(0, 0, p^{\star})$ 处的非竖直的支撑超平面。
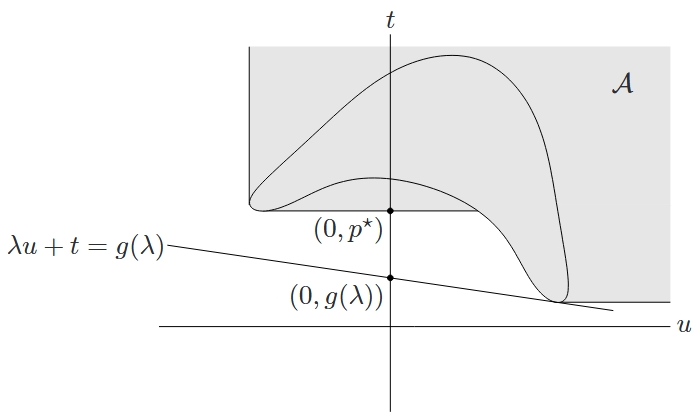
针对具有一个(不等式)约束的问题,对偶函数和下界 $g(\lambda) \leqslant p^{\star}$ 的几何解释。给定 $\lambda$,在 $\mathcal{A}$ 上极小化 $(\lambda, 1)^{\top}(u, t)$。这样可以得到斜率为 $-\lambda$ 的支撑超平面。此支撑超平面与坐标轴 $u = 0$ 的交点即为 $(0, g(\lambda))$。
在约束规则下强对偶性成立的证明
本文从略
多准则解释
多准则凸优化问题的每个 Pareto 最优解都是给定某个非负权向量 $\tilde{\lambda}$ 时函数
$$ \tilde{\lambda}^{\top} F(x)=f_{0}(x)+\sum_{i=1}^{m} \lambda_{i} f_{i}(x) $$的最小点,我们考虑集合
$$ \mathcal{A}=\left\{ t \in \mathbf{R}^{m+1} \mid \exists x \in \mathcal{D}, f_{i}(x) \leqslant t_{i}, i=0, \cdots, m \right\} $$这和研究 Lagrange 对偶问题时的定义一样,此时所需权向量也是集合在任意一个 Pareto 最优点处的支撑超平面。在多准则优化问题中,权向量的含义是目标函数的相对权重。当我们固定权向量的最后一个分量(和函数 $f_0$ 对应)为 $1$ 时,其他权向量分量的含义是相对 $f_0$ 的成本,即相对于目标函数的成本。