KKT 条件究其本质,是优化问题取得最优解的必要条件。下面我们首先从我们最熟悉的知识开始。
等式约束优化问题
我们在《高等数学》课程中学习过多元函数的极值问题,其中提到了 Lagrange 乘子法。其本质就是运用《凸优化》课程当中讲的 Lagrange 函数,求解等式优化问题。只不过《高等数学》课程中不涉及不等式约束,仅仅只有等式约束。为了更贴近也更容易回忆起《高等数学》所学内容,我们在这里仅考虑二元函数,并且只有一个等式约束。此时,这个约束优化问题记为
$$ \begin{aligned} \mathrm{min} \quad & f(x, y) \\ \mathrm{s.t.} \quad & g(x, y) = 0 \end{aligned} $$这里只有一个等式约束,因此只需要引入一个 Lagrange 乘子 $\lambda$ 即可
$$ L(x, y, \lambda) = f(x, y) + \lambda g(x, y) $$计算 $L$ 对 $x$、$y$ 和 $\lambda$ 的偏导数,并令它们都等于零,就可以得到最优解的必要条件
$$ \left\{ \begin{aligned} \frac{\partial L}{\partial x} &= f_x(x, y) + \lambda g_x(x, y) = 0 \\ \frac{\partial L}{\partial y} &= f_y(x, y) + \lambda g_y(x, y) = 0 \\ \frac{\partial L}{\partial \lambda} &= g(x, y) = 0 \end{aligned} \right. $$解上面的方程组就可以得到最优解 $(x^{\star}, y^{\star})$。
不等式约束优化问题
我们注意到,在刚才在求解的过程中,我们其实一点也不关心 $\lambda$ 的取值,因为那是我们引入的新变量,我们只关心原问题当中 $(x, y)$ 的取值。实际上,按照《高等数学》当中的方法求解出的 $\lambda$ 是无法判断其符号的。对于只含有等式约束的问题,这个问题并不重要。但是,对于含有不等式约束的问题来说,不等号的方向和引入的 Lagrange 乘子之间则是具有一定联系的。
我们先考虑仅含有一个不等式的约束的二元函数优化问题
$$ \begin{aligned} \mathrm{min} \quad & f(x, y) \\ \mathrm{s.t.} \quad & g(x, y) \leqslant 0 \end{aligned} $$我们先来讨论最优解 $(x^{\star}, y^{\star})$ 的情况,它应该有且仅有如下两种:
- $g(x^{\star}, y^{\star}) < 0$,说明最优解位于可行域的内部,称为内部解。此时约束条件是无效的。
- $g(x^{\star}, y^{\star}) = 0$,说明最优解位于可行域的边界,称为边界解。此时约束条件是有效的。
这两种情况的最优解具有不同的必要条件:
- 内部解:原问题退化为无约束优化问题,只要驻点 $(x^{\star}, y^{\star})$ 满足 $\nabla f=0$ 且 $\lambda = 0$。
- 边界解:原问题转变为等式约束优化问题,这与之前讨论的情况相同。可以证明的一点是,最优解处的 $f$ 和 $g$ 的梯度方向是反向,即 $\exists \lambda$ 使得 $\nabla f = - \lambda \nabla g$。这里 $\lambda$ 的正负性是有意义的。由于我们希望最小化 $f$,梯度 $\nabla f$ 的值表示函数值上升最快的方向,因而负梯度方向 $-\nabla f$ 应该指向可行域的内部。$\nabla g$ 指向可行域的外部,即 $g(x, y) > 0$ 的区域,因为约束 $g(x, y) \leqslant 0$。因此这里的 $\lambda \geqslant 0$,这就是之前几节讲的对偶可行性。
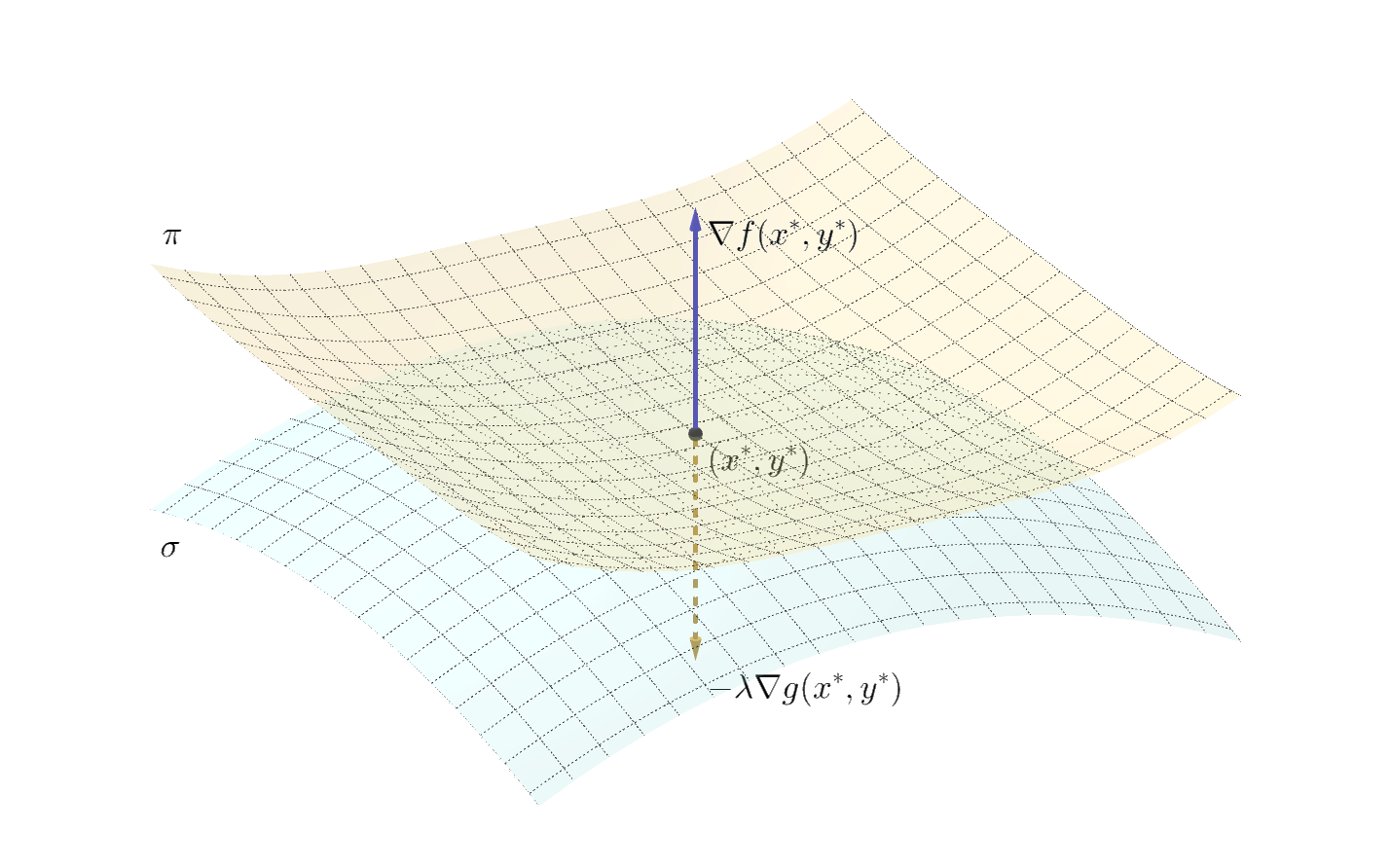
边界解的情况可以通过上图加深理解。图中表示的是二元函数 $f(x, y)$ 在不等式约束 $g(x, y) \leqslant 0$ 下的优化问题,并且最优解在边界的情况。如图所示,最优点即为平面 $\pi$(方程 $z = f(x, y)$)和平面 $\sigma$(方程 $g(x, y) = 0$)的交点。约束 $g(x, y) \leqslant 0$ 说明了可行域在平面 $\sigma$ 的下侧。梯度 $\nabla f$ 指向上方,负梯度 $-\nabla f$ 指向下方可行域内部。在最优解 $(x^{\star}, y^{\star})$ 处,$\nabla f$ 和 $\nabla g$ 共线。
更一般地,如果有多个不等式约束,对应到上图中就是有若干平面 $\sigma_1,\cdots,\sigma_p$,并且在最优点处 $\nabla f(x^{\star}, y^{\star})$ 可由有效约束对应的平面的支撑超平面的法向量的线性表示。即 $\exists \mu_1,\cdots,\mu_p \geqslant 0$,使得
$$ \nabla f(x^{\star}, y^{\star}) = -(\mu_1 \nabla g_1(x^{\star}, y^{\star}) + \cdots + \mu_p \nabla g_p(x^{\star}, y^{\star})) $$而不论是内部解还是边界解,$\lambda g(x, y) = 0$ 恒成立,这就是互补松弛性。
小结
回顾了等式约束优化和不等式约束优化之后,我们可以从中提炼出一种转化的思想:
- 无约束优化问题:令梯度向量为零即可。
- 等式约束优化问题:引入 Lagrange 乘子,将原目标函数转化为 Lagrange 函数,将原问题转化为无约束优化问题。
- 不等式约束优化问题:引入松弛变量,将原不等式约束函数转化为等式约束函数,将原问题转化为等式约束优化问题。
KKT 条件的本质
综合上面的讨论与分析,我们再来看看 KKT 条件:
$$ \begin{aligned} f_{i}\left(x^{\star}\right) &\leqslant 0, & i &=1, \cdots, m \\ h_{i}\left(x^{\star}\right) &=0, & i &=1, \cdots, p \\ \lambda_{i}^{\star} & \geqslant 0, & i &=1, \cdots, m \\ \lambda_{i}^{\star} f_{i}\left(x^{\star}\right) &=0, & i &=1, \cdots, m \\ \nabla f_{0}\left(x^{\star}\right)+\sum_{i=1}^{m} \lambda_{i}^{\star} \nabla f_{i}\left(x^{\star}\right)+\sum_{i=1}^{p} \nu_{i}^{\star} \nabla h_{i} \left(x^{\star}\right) &=0 & & \end{aligned} $$其中一个包含了四个条件,它们分别是:
- Lagrange 函数的定常方程式:上式最后一行 $\nabla L = 0$。
- 原始可行性:即满足等式约束和不等式约束,上式第一行 $f_{i}\left(x^{\star}\right) \leqslant 0$ 和第二行 $h_{i}\left(x^{\star}\right) =0$。
- 对偶可行性:即上式第三行 $\lambda_{i}^{\star} \geqslant 0$。
- 互补松弛性:即上式第四行 $\lambda_{i}^{\star} f_{i}\left(x^{\star}\right) =0$。
简单的例子
考虑下面的问题
$$ \begin{aligned} \mathrm{min} \quad & x^2 + y^2 \\ \mathrm{s.t.} \quad & x + y = 1 \\ \quad & y \leqslant \alpha \end{aligned} $$写出 Lagrange 函数
$$ L(x, y, \lambda, \nu) = x^2 + y^2 + \lambda(1 - x - y) + \nu(y - \alpha) $$KKT 条件方程组如下
$$ \left\{\begin{aligned} 2x - \lambda &= 0 & (1) \\ 2y - \lambda + \nu &= 0 & (2) \\ \nu &\geqslant 0 & (3) \\ \nu(y - \alpha) &= 0 & (4) \end{aligned}\right. $$分别由 (1) 式和 (2) 式求出
$$ \left\{\begin{aligned} x &= \frac{1}{2} \lambda & (5) \\ y &= \frac{1}{2} \lambda - \frac{1}{2} \nu & (6) \end{aligned}\right. $$代入等式约束 $x+y=1$,得到 $\lambda$ 和 $\nu$ 的函数关系
$$ \lambda = \frac{1}{2} \nu + 1 $$再代入式 (5) 和 (6) 中,消去 $\lambda$
$$ \left\{\begin{aligned} x &= \frac{1}{4} \nu + \frac{1}{2} & (7) \\ y &= -\frac{1}{4} \nu + \frac{1}{2} & (8) \end{aligned}\right. $$最后再加入不等式约束,得到
$$ \left\{\begin{aligned} \nu & \geqslant 2 - 4 \alpha \\ \nu & \geqslant 0 \end{aligned}\right. $$下面对参数 $\alpha$ 进行分类讨论:
- 若 $\alpha > \frac{1}{2}$,不难验证 $\nu = 0 > 2 - 4 \alpha$。此时满足所有的 KKT 条件,约束不等式是无效的。$x^{\star} = y^{\star} = \frac{1}{2}$ 是内部解。
- 若 $\alpha = \frac{1}{2}$,$\nu = 0 = 2 - 4 \alpha$。此时满足所有的 KKT 条件,约束不等式是有效的。$x^{\star} = y^{\star} = \frac{1}{2}$ 是边界解。
- 若 $\alpha < \frac{1}{2}$,$\nu = 2 - 4 \alpha > 0$。此时约束不等式是有效的。$x^{\star} = 1 - \alpha$,$y^{\star} = \alpha$。
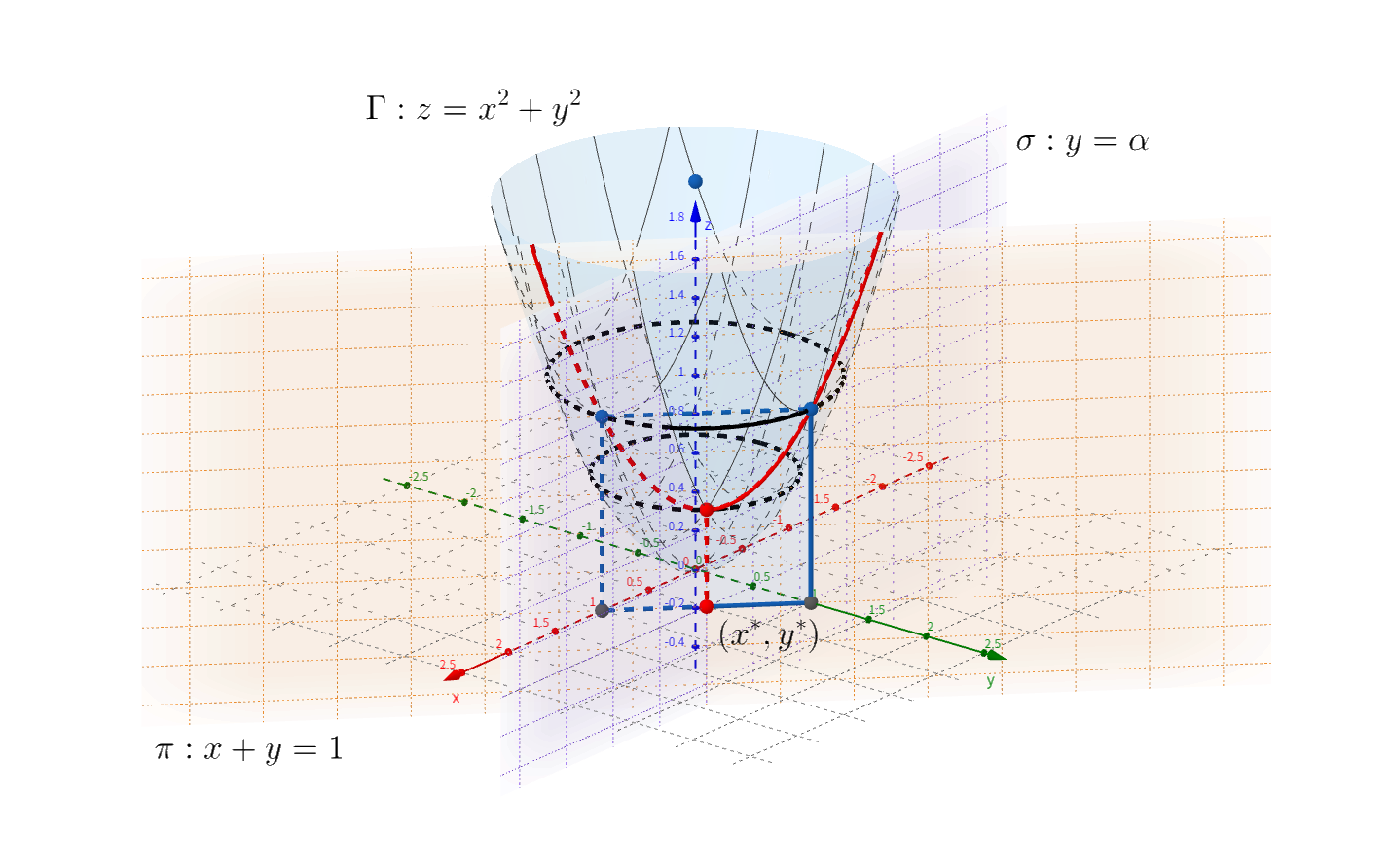
本题的几何意义如图所示。目标函数对应的曲面 $\Gamma$ 是(椭)圆抛物面,等式约束对应平面 $\pi$,不等式约束对应以平面 $\sigma$ 为边界的左半空间。曲面 $\Gamma$ 和平面 $\pi$ 的交线为图中的红色曲线(该曲线实际上是一个抛物线)。不考虑不等式约束,该优化问题的最优解为 $(x^{\star}, y^{\star}) = (\frac{1}{2}, \frac{1}{2})$,最优值为 $f(x^{\star}, y^{\star}) = \frac{1}{2}$,对应图中红点的坐标 $(\frac{1}{2}, \frac{1}{2}, \frac{1}{2})$。不等式约束实际上是让平面 $\alpha$ 沿 $y$ 轴方向平移,以 $\alpha = \frac{1}{2}$ 为界,可以分三种情况讨论。
参考