开集和闭集
对于 $x \in C \subseteq \mathbf{R}^n$,如果存在 $\epsilon > 0$ 使得
$$ \begin{align*} \{y \mid\|y-x\|_{2} \leqslant \epsilon\} \subseteq C \end{align*} $$即存在一个以 $x$ 为中心的完全包含于 $C$ 的球,则称 $x$ 为 $C$ 的内点。$C$ 的所有内点组成的集合称为 $C$ 的内部,记作 $\operatorname{int}C$。若 $\operatorname{int}C = C$,则称集合 $C$ 为开集。若集合 $C \subseteq \mathbf{R}^n$ 的补集 $\mathbf{R}^{n} \backslash C={x \in \mathbf{R}^{n} \mid x \notin C}$ 是开集,则称集合 $C$ 为闭集。
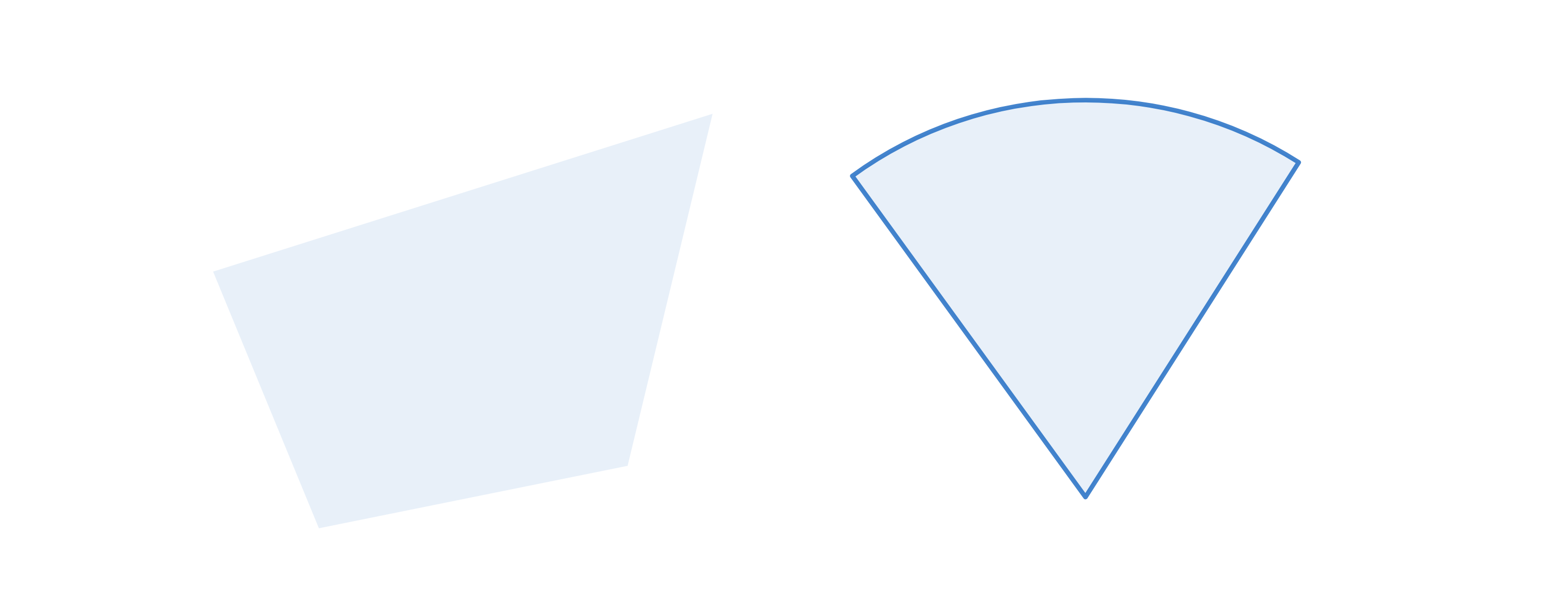
如图所示,在二维平面中,不包含边界的多边形是开集(左图所示),包含边界的扇形是闭集(右图所示)。实际上,开集和闭集的概念可以看作是实数集上开区间和闭区间在 $n$ 维空间中的推广。
闭包
$$ \begin{align*} \textbf{cl } C=\mathbf{R}^{n} \backslash \textbf{ int}(\mathbf{R}^{n} \backslash C) \end{align*} $$集合 $C$ 的闭包即为补集内部的补集。在上面的图中,左图不含边界的圆的闭包正好是右边包含边界的圆,而右边包含边界的圆的闭包正好是它本身。点 $x$ 属于 $C$ 的闭包的条件是:对于 $\forall \epsilon > 0$,$\exists y \in C$ 使得 $|x-y| _2 \leqslant \epsilon$。
边界
$$ \begin{align*} \textbf{bd } C=\textbf{cl } C \backslash \textbf{int } C \end{align*} $$显然,边界实际上就是集合的闭包去掉它所有的内点。我们可以用边界来刻画开集和闭集:
- 开集:不含有边界点,即 $C \cap \textbf{bd } C = \emptyset$。
- 闭集:包含边界,即 $\textbf{bd } C \in C$。
上确界和下确界
假定 $C \subseteq \mathbf{R}$。如果对 $\forall x \in C$,$\exists a \in \mathbf{R}$ 使得 $x \leqslant a$ 恒成立,则称 $a$ 为 $C$ 的上界。其中,使得 $x \leqslant a$ 成立的最小的 $a$ 称为最小上界或者上确界,记作 $\sup C$。
我们规定:
- $\sup \emptyset = - \infty$
- 当 $C$ 无上界时 $\sup C = \infty$
当 $\sup C \in C$ 时,我们说 $C$ 的上确界是可达的。
类似地,我们可以很容易给出下确界的定义。本文从略。