Dirichlet 积分

【问题】计算广义积分

$$ \int_{0}^{+\infty} \frac{\sin{x}}{x} \mathrm{d}x $$

---

解法一：构造含参变量函数

记

$$ I = \int_{0}^{+\infty} \frac{\sin{x}}{x} \mathrm{d}x $$

构造函数

$$ f(x) = \int_{0}^{+\infty} e^{-xt} \frac{\sin{t}}{t} \mathrm{d}t \quad (x \geqslant 0) $$

则

$$ \begin{align*} f(0) &= I \end{align*} $$

同时，利用定积分的基本性质，可以证明

$$ \begin{align*} 0 &\leqslant \left|\int_{0}^{+\infty} e^{-xt} \frac{\sin{t}}{t} \mathrm{d}t \right| \\ &\leqslant \int_{0}^{+\infty} e^{-xt} \left|\frac{\sin{t}}{t}\right| \mathrm{d}t \\ &\leqslant \int_{0}^{+\infty} e^{-xt} \mathrm{d}t \\ &= \frac{1}{x} \end{align*} $$

所以，根据极限的两边夹定理，当 $x \rightarrow +\infty$ 时

$$ \begin{align*} & \lim_{x \rightarrow +\infty} \left| f(x) \right| = 0 \\ \Longrightarrow & \lim_{x \rightarrow +\infty} f(x) = 0 \end{align*} $$

对函数 $f(x)$ 求一阶导数

$$ \begin{align*} f'(x) &= \int_{0}^{+\infty} \frac{\partial e^{-xt}}{\partial x} \cdot \frac{\sin{t}}{t} \mathrm{d}t \\ &= -t \int_{0}^{+\infty} e^{-xt} \frac{\sin{t}}{t} \mathrm{d}t \\ &= - \int_{0}^{+\infty} e^{-xt} \sin{t} \mathrm{d}t \end{align*} $$

然后我们令

$$ \Phi = - \int_{0}^{+\infty} e^{-xt} \sin{t} \mathrm{d}t $$

应用两次分部积分法

$$ \begin{align*} \Phi &= - \int_{0}^{+\infty} e^{-xt} \sin{t} \mathrm{d}t \\ &= \frac{1}{x} \int_{0}^{+\infty} \sin{t} \mathrm{d} e^{-xt} \\ &= \frac{1}{x} \left( e^{-xt} \sin{t} \Big|_{0}^{+\infty} - \int_{0}^{+\infty} e^{-xt} \mathrm{d} \sin{t} \right) \\ &= \frac{1}{x^{2}} \int_{0}^{+\infty} \cos{t} \mathrm{d} e^{-xt} \\ &= \frac{1}{x^{2}} \left(e^{-xt} \cos{t} \Big|_{0}^{+\infty} - \int_{0}^{+\infty} e^{-xt} \mathrm{d} \cos{t} \right) \\ &= - \frac{1}{x^2} \left( 1 + \Phi \right) \end{align*} $$

解得

$$ \Phi = - \frac{1}{x^2 + 1} $$

于是

$$ \begin{align*} f'(x) &= - \int_{0}^{+\infty} e^{-xt} \sin{t} \mathrm{d}t \\ &= - \frac{1}{x^2 + 1} \end{align*} $$

等式两边同时积分，由牛顿-莱布尼兹公式得

$$ \begin{align*} \int_{0}^{+\infty} f'(x) &= - \int_{0}^{+\infty} \frac{1}{x^2 + 1} \mathrm{d}x = - \arctan{x} \Big|_{0}^{+\infty} = -\frac{\pi}{2} \\ &= \lim_{x \rightarrow +\infty} f(x) - f(0) = -I \end{align*} $$

解得

$$ I = \frac{\pi}{2} $$

解法二：化为二重积分

考虑如下广义积分

$$ \begin{align*} \int_{0}^{+\infty} e^{-xy} \mathrm{d}y &= -\frac{1}{x} e^{-xy} \Big|_{0}^{+\infty} \\ &= \frac{1}{x} \end{align*} $$

将之代入原式得

$$ \begin{align*} \int_{0}^{+\infty} \frac{\sin{x}}{x} \mathrm{d}x &= \int_{0}^{+\infty} \sin{x} \left( \int_{0}^{+\infty} e^{-xy} \mathrm{d}y \right) \mathrm{d}x \\ &= \iint_{\mathbb{R}_{+}^{2}} \sin{x} e^{-xy} \mathrm{d}x \mathrm{d}y \end{align*} $$

化为二重积分后，交换积分次序，即先对 $x$ 积分

$$ \begin{align*} \int_{0}^{+\infty} \frac{\sin{x}}{x} \mathrm{d}x &= \int_{0}^{+\infty} \left( \int_{0}^{+\infty} \sin{x} e^{-xy} \mathrm{d}x \right) \mathrm{d}y \end{align*} $$

由解法一的计算结果可知，上式可化简为

$$ \begin{align*} \int_{0}^{+\infty} \frac{\sin{x}}{x} \mathrm{d}x &= \int_{0}^{+\infty} \frac{1}{y^2 + 1} \mathrm{d}y \\ &= \arctan{x} \Big|_{0}^{+\infty} \\ &= \frac{\pi}{2} \end{align*} $$

解法三：留数定理

根据欧拉公式可知

$$ \begin{align*} \sin{x} &= \frac{1}{2i}\left(e^{ix} - e^{-ix}\right) \end{align*} $$

所以

$$ \begin{align*} \int_{0}^{+\infty} \frac{\sin{x}}{x} \mathrm{d}x &= \frac{1}{2i} \int_{0}^{+\infty} \frac{e^{ix} - e^{-ix}}{x} \mathrm{d}x \\ &= \frac{1}{2i} \int_{0}^{+\infty} \frac{e^{ix}}{x} \mathrm{d}x - \frac{1}{2i} \int_{0}^{-\infty} \frac{e^{-ix}}{-x} \mathrm{d}(-x) \\ &= \frac{1}{2i} \int_{0}^{+\infty} \frac{e^{ix}}{x} \mathrm{d}x + \frac{1}{2i} \int_{-\infty}^{0} \frac{e^{ix}}{x} \mathrm{d}x \\ &= \frac{1}{2i} \int_{-\infty}^{+\infty} \frac{e^{ix}}{x} \mathrm{d}x \end{align*} $$

构造复变函数

$$ f(z) = \frac{e^{iz}}{z} $$

它有一个孤立奇点 $z_0=0$。由留数定理得

$$ \begin{align*} \int_{0}^{+\infty} \frac{\sin{x}}{x} \mathrm{d}x &= \frac{1}{2i} \int_{-\infty}^{+\infty} \frac{e^{ix}}{x} \mathrm{d}x \\ &= \frac{1}{2i} \cdot i \pi \mathrm{Res}[f(z), z_0] \\ &= \frac{\pi}{2} \mathrm{Res}[f(z), z_0] \end{align*} $$

注意到此处在运用留数定理时，被积函数是定义在实数域上的。实轴上的奇点具有对称性，积分路径（即实轴）的上半部分和下半部分对积分的贡献是相等的。因此，在应用留数定理时只需考虑上半复平面的情况即可。

$$ \begin{align*} \int_{0}^{+\infty} \frac{\sin{x}}{x} \mathrm{d}x &= \frac{\pi}{2} \mathrm{Res}[f(z), z_0] \\ &= \frac{\pi}{2} \cdot \frac{1}{2 \pi i} \oint_{|z|=\varepsilon} f(z) \mathrm{d}z \\ &= \frac{1}{4i} \oint_{|z|=\varepsilon} \frac{e^{iz}}{z} \mathrm{d}z \end{align*} $$

其中，$\varepsilon > 0$ 是一个任意小的常数。所以曲线积分的路径是一个半径为 $\varepsilon$ 的圆。

作变量变换 $z = iz$，相当于将复平面顺时针旋转了 90°。但是这并没有改变曲线积分的路径，即

$$ \begin{align*} |z| &= \varepsilon \\ \Longleftrightarrow |iz| &= \varepsilon \end{align*} $$

下面来计算这个环路上的积分

$$ \begin{align*} \oint_{|z|=\varepsilon} \frac{e^{iz}}{z} \mathrm{d}z &= \oint_{|z|=\varepsilon} \frac{e^{iz}}{iz} \mathrm{d}(iz) \\ &= \oint_{|z|=\varepsilon} \frac{e^{z}}{z} \mathrm{d}z \\ &= \oint_{|z|=\varepsilon} \frac{1}{z} \left( \sum_{n=0}^{\infty} \frac{z^n}{n!} \right) \mathrm{d}z \\ &= \oint_{|z|=\varepsilon} \left( \frac{1}{z} + \sum_{n=1}^{\infty} \frac{z^{n-1}}{n!} \right) \mathrm{d}z \\ &= \oint_{|z|=\varepsilon} \frac{1}{z} \mathrm{d}z + \oint_{|z|=\varepsilon} \sum_{n=1}^{\infty} \frac{z^{n-1}}{n!} \mathrm{d}z \end{align*} $$

由柯西积分定理可知，如果环路所围成的区域是单连通区域，即没有孤立奇点，那么积分结果为零。这意味着

$$ \begin{align*} \oint_{|z|=\varepsilon} \sum_{n=1}^{\infty} \frac{z^{n-1}}{n!} \mathrm{d}z &= 0 \end{align*} $$

那么，下面只需求解

$$ \begin{align*} \oint_{|z|=\varepsilon} \frac{1}{z} \mathrm{d}z \end{align*} $$

作变量变换 $z = e^{i \theta}$，得到

$$ \begin{align*} \oint_{|z|=\varepsilon} \frac{1}{z} \mathrm{d}z &= \int_{0}^{2 \pi} \frac{1}{e^{i \theta}} \mathrm{d}(e^{i \theta}) \\ &= i \int_{0}^{2 \pi} \mathrm{d}\theta \\ &= 2 \pi i \end{align*} $$

于是

$$ \begin{align*} \int_{0}^{+\infty} \frac{\sin{x}}{x} \mathrm{d}x &= \frac{1}{4i} \oint_{|z|=\varepsilon} \frac{e^{iz}}{z} \mathrm{d}z \\ &= \frac{1}{4i} \cdot 2 \pi i \\ &= \frac{\pi}{2} \end{align*} $$

解法四：柯西积分定理

由解法三可知

$$ \begin{align*} \int_{0}^{+\infty} \frac{\sin{x}}{x} \mathrm{d}x &= \frac{1}{2i} \int_{-\infty}^{+\infty} \frac{e^{ix}}{x} \mathrm{d}x \\ &= \frac{1}{2i} \left( \int_{-\infty}^{0} \frac{e^{ix}}{x} \mathrm{d}x + \int_{0}^{+\infty} \frac{e^{ix}}{x} \mathrm{d}x \right) \end{align*} $$

定义复变函数

$$ \begin{align*} f(z) = \frac{e^{iz}}{z} \end{align*} $$

为了挖掉 $f(z)$ 的孤立奇点 $z_0=0$，定义 $f(z)$ 的积分路径 $C$ 为

$$ \begin{align*} C_{R}: |z| &= R, \arg z \in [0, \pi] \\ C_{r}: |z| &= r, \arg z \in [0, \pi] \\ Im(z) &= 0, |z| \in [r, R] \end{align*} $$

所构成的正向闭曲线，如下图所示

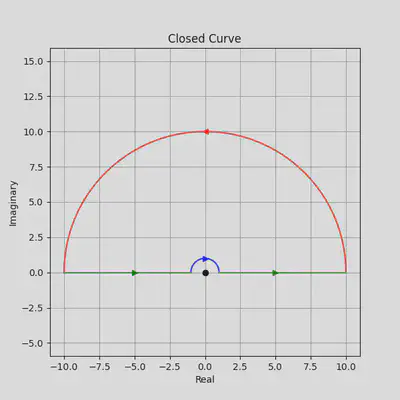
由柯西积分定理得

$$ \begin{align*} \oint_{C} \frac{e^{iz}}{z} \mathrm{d}z &= \int_{C_{R}} \frac{e^{iz}}{z} \mathrm{d}z + \int_{-R}^{-r} \frac{e^{ix}}{x} \mathrm{d}x + \int_{C_{r}} \frac{e^{iz}}{z} \mathrm{d}z + \int_{r}^{R} \frac{e^{ix}}{x} \mathrm{d}x \\ &= 0 \end{align*} $$

那么

$$ \begin{align*} \int_{0}^{+\infty} \frac{\sin{x}}{x} \mathrm{d}x &= \frac{1}{2i} \lim_{\substack{r \to 0 \\ R \to +\infty}} \left( \int_{-R}^{-r} \frac{e^{ix}}{x} \mathrm{d}x + \int_{r}^{R} \frac{e^{ix}}{x} \mathrm{d}x \right) \\ &= -\frac{1}{2i} \left( \lim_{R \to +\infty} \int_{C_{R}} \frac{e^{iz}}{z} \mathrm{d}z + \lim_{r \to 0} \int_{C_{r}} \frac{e^{iz}}{z} \mathrm{d}z \tag{*} \right) \end{align*} $$

下面分别计算这两个曲线积分。首先计算外环路径上的积分

$$ \begin{align*} \int_{C_{R}} \frac{e^{iz}}{z} \mathrm{d}z &\leqslant \int_{C_{R}} \frac{\left|e^{iz}\right|}{|z|} \mathrm{d}s \\ &= \frac{1}{R} \int_{C_{R}} \left|e^{ix-y}\right| \mathrm{d}s \\ &= \frac{1}{R} \int_{C_{R}} e^{-y} \mathrm{d}s \\ &= \int_{0}^{\pi} e^{-R \sin{\theta}} \mathrm{d}\theta \\ &= 2 \int_{0}^{\frac{\pi}{2}} e^{-R \sin{\theta}} \mathrm{d}\theta \\ &\leqslant 2 \int_{0}^{\frac{\pi}{2}} e^{-\frac{2R}{\pi} \theta} \mathrm{d}\theta \\ &= -\frac{\pi}{R} e^{-\frac{2R}{\pi} \theta} \Big|_0^{\frac{\pi}{2}} \\ &= \frac{\pi}{R} \left(1 - e^{-R} \right) \end{align*} $$

这里进行了两次放大。第一次是利用积分的基本性质（保号性的推论），第二次是将曲线简化为割线。具体来说，对于 $\theta \in [0, \frac{\pi}{2}]$

$$ \sin{\theta} \geqslant \frac{2}{\pi} \theta $$

而根据被积函数的单调性，达到化曲为直、放大结果的目的。

所以当 $R \to +\infty$ 时

$$ \begin{align*} \lim_{R \to +\infty} \int_{C_{R}} \frac{e^{iz}}{z} \mathrm{d}z &= 0 \tag{1} \end{align*} $$

下面继续计算内环路径上的积分。我们尝试将 $f(z)$ 展开成洛朗级数

$$ \begin{align*} \int_{C_{r}} \frac{e^{iz}}{z} \mathrm{d}z &= \int_{C_{r}} \frac{1}{z} \sum_{n=0}^{\infty} \frac{i^{n}z^{n}}{n!} \mathrm{d}z \\ &= \int_{C_{r}} \left( \frac{1}{z} + \sum_{n=1}^{\infty} \frac{i^{n}z^{n-1}}{n!} \right) \mathrm{d}z \\ &= \int_{C_{r}} \frac{1}{z} \mathrm{d}z + \int_{C_{r}} \sum_{n=1}^{\infty} \frac{i^{n}z^{n-1}}{n!} \mathrm{d}z \\ &= \int_{\pi}^{0} \frac{ire^{i \theta}}{re^{i \theta}} \mathrm{d}\theta + \int_{C_{r}} \sum_{n=1}^{\infty} \frac{i^{n}z^{n-1}}{n!} \mathrm{d}z \\ &= \int_{C_{r}} \sum_{n=1}^{\infty} \frac{i^{n}z^{n-1}}{n!} \mathrm{d}z - i\pi \end{align*} $$

由于被积函数中需要展开的部分只有指数函数，相当于是作了泰勒级数展开。

下面研究正幂项的积分，令

$$ \varphi(z) = \sum_{n=1}^{\infty} \frac{i^{n}z^{n-1}}{n!} \mathrm{d}z $$

则

$$ \begin{align*} \left| \int_{C_{r}} \varphi(z) \mathrm{d}z \right| &\leqslant \int_{C_{r}} \left| \varphi(z) \right| \mathrm{d}s \\ &= \int_{C_{r}} \left| \sum_{n=1}^{\infty} \frac{i}{n} \cdot \frac{i^{n-1}z^{n-1}}{(n-1)!} \right| \mathrm{d}s \\ &\leqslant \int_{C_{r}} \left| \sum_{n=1}^{\infty} \frac{i^{n-1}z^{n-1}}{(n-1)!}\right| \mathrm{d}s \\ &= \int_{C_{r}} \left| e^{iz} \right| \mathrm{d}s \\ &= r \int_{0}^{\pi} \mathrm{d}\theta \\ &= \pi r \end{align*} $$

这里一共进行了两次放大。第一次是利用积分的基本性质（保号性的推论），第二次是将求和的每一项都放大 $n$ 倍。

所以当 $r \to 0$ 时

$$ \begin{align*} \lim_{r \to 0} \int_{C_{r}} \varphi(z) \mathrm{d}z &= 0 \end{align*} $$

于是

$$ \begin{align*} \lim_{r \to 0} \int_{C_{r}} \frac{e^{iz}}{z} \mathrm{d}z &= \lim_{r \to 0} \int_{C_{r}} \sum_{n=1}^{\infty} \frac{i^{n}z^{n-1}}{n!} \mathrm{d}z - i\pi \\ &= -i \pi \tag{2} \end{align*} $$

将 (1), (2) 这两个积分的结果代入原式 (*)，得到

$$ \begin{align*} \int_{0}^{+\infty} \frac{\sin{x}}{x} \mathrm{d}x &= -\frac{1}{2i} \left( \lim_{R \to +\infty} \int_{C_{R}} \frac{e^{iz}}{z} \mathrm{d}z + \lim_{r \to 0} \int_{C_{r}} \frac{e^{iz}}{z} \mathrm{d}z \right) \\ &= \left(-\frac{1}{2i} \right) \cdot (-i \pi) \\ &= \frac{\pi}{2} \end{align*} $$

附：闭曲线作图相关代码

解法五：傅里叶变换

考虑如下定积分

$$ \begin{align*} \frac{1}{2\pi} \int_{-1}^{1} \pi e^{iwt} \mathrm{d}w &= \frac{1}{2it} e^{iwt} \Big|_{-1}^{1} \\ &= \frac{1}{2it} \left( e^{it} - e^{-it} \right) \\ &= \frac{\sin{t}}{t} \end{align*} $$

这是一个傅里叶逆变换的表达式，它充分地说明了频域内的信号

$$ F(w) = \left\{ \begin{array}{ll} \pi, & -1 \leqslant w \leqslant 1 \\ 0, & \mathrm{else} \end{array} \right. $$

在时域内对应的信号就是被积函数 $f(t)$，即

$$ \begin{align*} F(w) &= \mathscr{F}(f(t)) \\ &= \int_{-\infty}^{+\infty} f(t) e^{-iwt} \mathrm{d}t \\ &= \int_{-1}^{1} \frac{\sin{t}}{t} e^{-iwt} \mathrm{d}t \\ &= \pi \end{align*} $$

令 $w=0$，得到

$$ \begin{align*} F(0) &= \int_{-\infty}^{+\infty} \frac{\sin{t}}{t} \mathrm{d}t \\ &= \pi \end{align*} $$

又因为 $f(x)$ 是偶函数，所以

$$ \begin{align*} \int_{0}^{+\infty} \frac{\sin{x}}{x} \mathrm{d}x &= \frac{1}{2} \int_{-\infty}^{+\infty} \frac{\sin{x}}{x} \mathrm{d}x \\ &= \frac{\pi}{2} \end{align*} $$

解法六：拉普拉斯变换

构造一个以 $t$ 为变量的函数 $f(t)$

$$ \begin{align*} f(t) = \int_{0}^{+\infty} \frac{\sin{tx}}{x} \mathrm{d}x \quad (t > 0) \end{align*} $$

则原式的值即为 $f(1)$。对 $f(t)$ 作拉普拉斯变换得

$$ \begin{align*} F(s) = \mathscr{L}(f(t)) &= \int_{0}^{+\infty} \left( \int_{0}^{+\infty} \frac{\sin{tx}}{x} \mathrm{d}x \right) e^{-st} \mathrm{d}t \\ &= \iint_{\mathbb{R}_{+}^{2}} \frac{\sin{tx}}{x} e^{-st} \mathrm{d}x \mathrm{d}t \\ &= \int_{0}^{+\infty} \frac{1}{x} \left( \int_{0}^{+\infty} \sin{tx} e^{-st} \mathrm{d}t \right) \mathrm{d}x \end{align*} $$

交换二重积分的积分次序后，使用两次分部积分法计算内层积分

$$ \begin{align*} I &= \int_{0}^{+\infty} \sin{tx} e^{-st} \mathrm{d}t \\ &= -\frac{1}{s} \int_{0}^{+\infty} \sin{tx} \mathrm{d} e^{-st} \\ &= -\frac{1}{s} \left( \sin{tx} e^{-st} \Big|_{0}^{+\infty} - x \int_{0}^{+\infty} \cos{tx} e^{-st} \mathrm{d}t \right) \\ &= \frac{x}{s} \int_{0}^{+\infty} \cos{tx} e^{-st} \mathrm{d}t \\ &= -\frac{x}{s^2} \int_{0}^{+\infty} \cos{tx} \mathrm{d} e^{-st} \\ &= -\frac{x}{s^2} \left( \cos{tx} e^{-st} \Big|_{0}^{+\infty} + x \int_{0}^{+\infty} \sin{tx} e^{-st} \mathrm{d}t \right) \\ &= -\frac{x}{s^2} \left(xI - 1\right) \end{align*} $$

解得

$$ \begin{align*} I = \frac{x}{x^2 + s^2} \end{align*} $$

代入原式得

$$ \begin{align*} F(s) &= \int_{0}^{+\infty} \frac{1}{x} \cdot \frac{x}{x^2 + s^2} \mathrm{d}x \\ &= \frac{1}{s} \int_{0}^{+\infty} \frac{1}{\left(\frac{x}{s}\right)^{2} + 1} \mathrm{d} \frac{x}{s} \\ &= \frac{1}{s} \arctan(\frac{x}{s}) \Big|_{0}^{+\infty} \\ &= \frac{\pi}{2s} \end{align*} $$

于是，再将 $F(s)$ 作拉普拉斯逆变换得

$$ \begin{align*} f(t) &= \mathscr{L}^{-1}(F(s)) \\ &= \frac{\pi}{2} \mathscr{L}^{-1}(\frac{1}{s}) \\ &= \frac{\pi}{2} \cdot \frac{1}{4\pi j} \int_{\beta-j\infty}^{\beta+j\infty} \frac{e^{-st}}{s} \mathrm{d}s \end{align*} $$

查阅拉普拉斯变换对可知

$$ \begin{align*} \frac{1}{s} \longleftrightarrow u(t) \end{align*} $$

其中 $u(t)$ 是单位阶跃函数

$$ u(t) = \left\{\begin{array}{rr} 0, & t < 0 \\ 1, & t > 0 \end{array} \right. $$

所以 $f(t)$ 的表达式为

$$ \begin{align*} f(t) &= \frac{\pi}{2} \mathscr{L}^{-1}(\frac{1}{s}) \\ &= \left\{ \begin{array}{rr} 0, & t < 0 \\ \frac{\pi}{2}, & t > 0 \end{array} \right. \end{align*} $$

于是

$$ \begin{align*} \int_{0}^{+\infty} \frac{\sin{x}}{x} \mathrm{d}x = f(1) = \frac{\pi}{2} \end{align*} $$

特别地，我们通过拉普拉斯逆变换的方法发现，对于任意的 $n > 0$，有

$$ \begin{align*} \int_{0}^{+\infty} \frac{\sin{nx}}{x} \mathrm{d}x = \frac{\pi}{2} \end{align*} $$