大模型的参数量及其计算访存开销的理论分析
推理服务系统的根本目标在于降低时延和提高吞吐量,LLM 推理的优化也是如此。首字时延(Time To First Token, TTFT)和吐字时延(Time Per Output Token, TPOT)就是两个非常重要的指标。如何优化 LLM 推理的这两个指标成为近年来学术界热议的问题。在研究这个问题之前,有必要深入理解 LLM 架构,分析其参数量和计算访存开销。
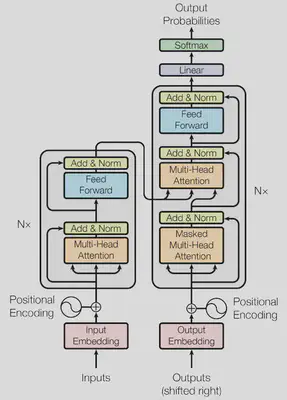
Transformer1 是一种 Encoder-Decoder 结构的模型,它被认为是 LLM 的基础模型。此后,诸如 Encoder only 模型(BERT2)、Decoder only 模型(GPT3)、Encoder-Decoder 模型都是在 Transformer 基础之上的变体。但不论是何种结构的 LLM,其内部都主要包含如下 block:
- Multi-Head Self-Attention:多头自注意力
- Feed-Forward:前馈网络
- Add & LayerNorm:层归一化
此外,还包括如下一些 block:
- Token Embedding:词嵌入
- Position Embedding:位置嵌入
- Linear:输出的线性层
- Softmax:激活函数
LLM 超参数定义如下:
| 超参数 | 符号表示 | Transformer 中的大小 |
|---|---|---|
| $d_{\textrm{model} }$ | M | 512 |
| $d_k(d_v)$ | D | 64 |
| Head | H | 8 |
| $d_{ff}$ | F | 2048 |
根据论文中的定义,其中 $M = HD$,$F = 4M$。
参数量理论计算
MHA
多头自注意力模块的每个 head 都需要 2 次 Self-Attention 的计算,即
$$ \text{Attention}(Q, K, V) = \text{Softmax}(\frac{QK^{\top}}{\sqrt{d_k}})V $$在那之前,需要将每个 token 从 $d_{\textrm{model}}$ 维映射到 $d_k(d_v)$ 维。(在 Transformer 模型中,$d_{\textrm{model}} = 512$,而 $d_k = d_v = \frac{d_{\textrm{model}}}{h} = 64$,这里 $h = 8$。)所以,输入的 $Q, K, V$ 向量都需要进行投影操作,共需 3 个线性变换矩阵 $W_K, W_Q, W_V$,维度均为 (M, D)。
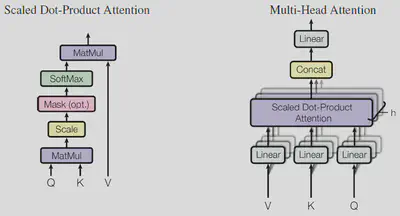
最终将每个 head 拼接起来,得到 $d_v \times h = d_{\textrm{model}}$ 维。这个结果再投影到 $d_{\textrm{model}}$ 维,需 1 个线性变换矩阵 $W_O$,维度为 (M, M)。即
因此,多头自注意力模块的总参数量为
$$ \begin{align*} & (d_{\textrm{model}} \times d_{qkv} + d_{qkv}) \times 3 \times h + (d_{\textrm{model}} \times d_{\textrm{model}} + d_{\textrm{model}}) \\ =\ & 4 (d_{\textrm{model}}^2 + d_{\textrm{model}}) \end{align*} $$在 $d_{ff}$ 很大的情况下,可以近似认为参数量为 $4d_{\textrm{model}}^2$。
FFN
前馈网络模块由 2 个全连接层,即
$$ \begin{align*} \text{FFN}(x) = \text{ReLU}(xW_1 + b_1)W_2 + b_2 \end{align*} $$其中隐藏层 $d_{ff}$ 的维度一般是 $d_{\textrm{model}}$ 的 4 倍。所以参数矩阵 $W_{in}, W_{out}$ 的维度分别为 (M, F) 和 (F, M)。因此,前馈网络模块的总参数量为
Add & LayerNorm
这一模块包含两个操作,一是 Add,即残差连接;二是 Layer Normalization,即
$$ \begin{align*} y = \frac{x - \mu}{\sigma + \epsilon} \times \gamma + \beta \end{align*} $$其中,$\mu$ 为均值,$\sigma$ 为标准差,$\epsilon$ 为定值,$\gamma$ 为缩放因子,$\beta$ 为偏移因子。$\gamma, \beta$ 是需要学习的参数,是 (1, M) 维的向量。因此,这部分参数量为
Embedding
Token Embedding 过程包含参数,参数量取决于训练数据 token 的数量 vocab_size。参数矩阵的维度为 (vocab_size, M)。
而 Positional Embedding 采用三角函数计算,即
$$ \begin{align*} PE_{(pos, 2i)} &= \sin (pos / 10000^{2i / d_{\textrm{model}}}) \\ PE_{(pos, 2i+1)} &= \cos (pos / 10000^{2i / d_{\textrm{model}}}) \end{align*} $$此过程不需要学习,因此没有参数。
Linear & Softmax
从最后一个编码器输出的结果需要经过一个线性层,通过 Softmax 化为概率分布后,选择最大概率的 token 输出。因此,线性层的参数矩阵具有 (M, vocab_size) 维。这部分的参数量为
参数量估算
LLM 总参数量为上述各部分参数量之和。不考虑输入和输出,按照 GPT 的架构,即 Decoder only,每个 Decoder 共 1 个 MHA、1 个 FFN 和 2 个 Add & LayerNorm。这样我们可以得到参数量为
$$ \begin{align*} & 4 (d_{\textrm{model}}^2 + d_{\textrm{model}}) + \\ & 2 d_{\textrm{model}} d_{ff} + d_{\textrm{model}} + d_{ff} + \\ & 2 \times d_{\textrm{model}} \times 2 \\ \end{align*} $$这里我们继续简化,令 $d_{ff} = 4d_{\textrm{model}} = 4d$,得到
$$ \begin{align*} & 4 (d^2 + d) + 2d \times 4d + d + 4d +2d \times 2 \\ =\ & 12d^2 + 13d \end{align*} $$当 $d_{\textrm{model}}$ 较大时,Encoder 和 Decoder 部分的参数量和其他部分相比远远更大。因此,要快速估计 LLM 的参数量,一般可以采用 $12d_{\textrm{model}}^2$ 作为估计值。
验证参数量
Transformer
按照上述计算方法,我们首先验证 Transformer 的参数量。
首先,计算一个 Encoder 的参数量。一个 Encoder 包含 1 个 MHA block、1 个 FFN block 和 2 个 Add & LayerNorm,即
$$ \begin{align*} & 4 (d_{\textrm{model}}^2 + d_{\textrm{model}}) + \\ & 2 d_{\textrm{model}} d_{ff} + d_{\textrm{model}} + d_{ff} + \\ & 2 \times d_{\textrm{model}} \times 2 \\ =\ & 4 \times 512 \times (512+1) + \\ & 2 \times 512 \times 2048 + 512 + 2048 + \\ & 2 \times 512 \times 2 \\ =\ & 3,152,384 \end{align*} $$接下来,计算一个 Decoder 的参数量。一个 Decoder 包含 2 个 MHA block、1 个 FFN block 和 3 个 Add & LayerNorm,即
$$ \begin{align*} & 4 (d_{\textrm{model}}^2 + d_{\textrm{model}}) \times 2 + \\ & 2 d_{\textrm{model}} d_{ff} + d_{\textrm{model}} + d_{ff} + \\ & 2 \times d_{\textrm{model}} \times 3 \\ =\ & 4 \times 512 \times (512+1) \times 2 + \\ & 2 \times 512 \times 2048 + 512 + 2048 + \\ & 2 \times 512 \times 3 \\ =\ & 4,204,032 \end{align*} $$上面计算的只是一个 Encoder 或 Decoder 的参数量。Transformer 的 Encoder-Decoder 的数量均为 6 个。
除此之外,从最后一个编码器输出的结果需要经过一个线性层,通过 Softmax 化为概率分布后,选择最大概率的 token 输出。因此,线性层的参数矩阵具有 (M, vocab_size) 维。在 Transformer 论文中,训练所用的英语和德语对照表的 token 数量为 37,000 个。
因此,不考虑 Embedding,Transformer 的参数量为
$$ \begin{align*} & (3,152,384 + 4,204,032) \times 6 + 37,000 \times 512 \\ =\ & 63,082,496 \end{align*} $$这和论文中给出的 65M 的参数量在同一个量级上。只不过,这里没有考虑输入和输出部分的参数量。如果模型足够大,那么参数量主要取决于 Encoder 和 Decoder 部分。
LLaMA
LLaMA4 是基于 Transformer 的 Decoder only 模型。考虑到 LLaMA 是参数量远大于 Transformer 的 LLM,所以我们采用估算法,可以得到下表:
| Model | $d_{\textrm{model}}$ | Layer | 采用 $12d_{\textrm{model}}^2$ 估算 | 采用 $12d_{\textrm{model}}^2 + 13d_{\textrm{model}}$ 估算 |
|---|---|---|---|---|
| LLaMA-7B | 4096 | 32 | 6,442,450,944 | 6,444,154,880 |
| LLaMA-13B | 5120 | 40 | 12,582,912,000 | 12,585,574,400 |
| LLaMA-30B | 6656 | 60 | 31,897,681,920 | 31,902,873,600 |
| LLaMA-65B | 8192 | 80 | 64,424,509,440 | 64,433,029,120 |
可见,估算值和论文给定的参数量相差无几。同时也说明,LLM 参数量越大,Encoder 和 Decoder 部分的参数量占比也就越大。可以基本上忽略输入输出部分的参数。
计算访存开销
首先需要给出如下两个定义:
- FLOPS (Floating Point Operations Per Second): 每秒浮点运算次数,用于衡量模型计算开销。
- MOPS (Memory Operations Per Second): 每秒内存访问次数,用于衡量模型访存(I/O)开销。
一般地,如果一个系统在单位时间内访存次数越小而计算次数越多,那么该系统的吞吐量就越大。定义算术强度(Arithmetic Intensity5)为
$$ \begin{align*} \text{Arithmetic Intensity} = \frac{\text{FLOPS}}{\text{MOPS}} \end{align*} $$显然,算术强度越大,系统的吞吐量越高。
全量推理
全量推理阶段,即输入一个完整的 sequence,到输出第一个 token 的过程。其计算和访存开销与 sequence length 和 batch size 直接相关,分别用 $S_{in}$(下面简写为 $S$)和 $B$ 来分别表示其大小。
对于 MHA 的 4 个 proj 算子,即 $W_Q, W_K, W_V, W_O$,其映射的维度都是一致的,即从 $d_{\mathrm{model}}$ 到 $\mathrm{head} \times d_{k}$(或反过来)。这部分的 FLOPS 和 $B, S, M, H, D$ 成正比,即
由于需要把模型权重和中间激活 tensor 都加载到显存中,其 MOPS 由 2 个部分组成,即
$$ \begin{align*} \text{MOPS} & \propto 2BSM + MHD \\ &= 2BSM + M^2 \end{align*} $$其中,常数 $2$ 表示一对显存读写操作,因为中间激活 tensor 需要先读取,再将结果写入显存。
对于 Self-Attention 计算,$Q \times K$ 和 Score(用 $P$ 表示)$\times V$ 这 2 个线性算子的 FLOPS 与 $B, S^2, H, D$ 成正比,即
$$ \begin{align*} \text{FLOPS} & \propto BS^2HD \\ &= BS^2M \end{align*} $$不过,由于 Self-Attention 没有模型参数,其 MOPS 由 2 个部分组成,即读取 $Q$ 和 $K$ 向量,将结果写入显存,即
$$ \begin{align*} \text{MOPS} & \propto 2BSHD + BS^2H \\ &= 2BSM + BS^2H \end{align*} $$由于 Self-Attention 本质上是计算余弦距离,每个 head 内的向量计算的实际上是内积。这个过程需要额外的多次访存,以存储中间结果。所以,这部分的访存开销和 $B, S^2, H$ 成正比。
最后,对于 FFN 的 2 个线性算子,即 $W_{in}, W_{out}$ 2 个 MLP 层,其 FLOPS 与 $B, S, M, F$ 成正比,即
$$ \begin{align*} \text{FLOPS} & \propto BSMF + BSMF \\ &= 8BSM^2 \end{align*} $$其中,加号两边的部分虽然一样,但它们分别表示权重矩阵 $W_{in}, W_{out}$ 和偏置向量 $b_{in}, b_{out}$。
同理,和 MHA 的 4 个 proj 算子类似,FFN 的 MOPS 也由 2 个部分组成,即
综上所述,对于 Encoder 的 8 个线性算子,其 FLOPS、MOPS 和算术强度如下表6所示:
| Stage | FLOPS | MOPS | Arithmetic Intensity |
|---|---|---|---|
| $Q \times W_Q$ | $O(BSM^2)$ | $O(2BSM+M^2)$ | $$O\left(\frac{1}{\frac{2}{M}+\frac{1}{BS} }\right)$$ |
| $K \times W_K$ | $O(BSM^2)$ | $O(2BSM+M^2)$ | $$O\left(\frac{1}{\frac{2}{M}+\frac{1}{BS} }\right)$$ |
| $V \times W_V$ | $O(BSM^2)$ | $O(2BSM+M^2)$ | $$O\left(\frac{1}{\frac{2}{M}+\frac{1}{BS} }\right)$$ |
| $Q \times K$ | $O(BS^2M)$ | $O(2BSM+BS^2H)$ | $$O\left(\frac{1}{\frac{1}{D}+\frac{1}{S} }\right)$$ |
| $P \times V$ | $O(BS^2M)$ | $O(2BSM+BS^2H)$ | $$O\left(\frac{1}{\frac{1}{D}+\frac{1}{S} }\right)$$ |
| $A \times W_O$ | $O(BSM^2)$ | $O(2BSM+M^2)$ | $$O\left(\frac{1}{\frac{2}{M}+\frac{1}{BS} }\right)$$ |
| $F \times W_{in}$ | $O(8BSM^2)$ | $O(BSM+4M^2)$ | $$O\left(\frac{8}{\frac{1}{M}+\frac{4}{BS} }\right)$$ |
| $F \times W_{out}$ | $O(8BSM^2)$ | $O(BSM+4M^2)$ | $$O\left(\frac{8}{\frac{1}{M}+\frac{4}{BS} }\right)$$ |
上表给出了 LLM 主要的 8 个线性算子的 FLOPS、MOPS 和算术强度,这些开销在 LLM 推理过程中占主导地位。具体来说,这 8 个线性算子可以分为如下两类:
proj:即 Projection 投影,是激活矩阵和权重矩阵相乘的过程。包括 MHA block 的 $Q \times W_Q, K \times W_K, V \times W_V$ 和 $A \times W_O$ 以及 FFN block 的两个 MLP 层。act-to-act:即 MHA block 的两次自注意力计算 $Q \times K$ 和 $P \times V$。
通过上表,我们可以得出如下几点结论:
- 序列长度和批量大小对计算和访存开销的影响成正比。
- $d_{\textrm{model}}$ 对
proj算子的 FLOPS 和 MOPS 都具有二次的影响, - 序列长度对
act-to-act算子的 FLOPS 和 MOPS 都具有二次的影响。在序列长度较小时,act-to-act算子的计算量较小;但在序列长度较大时,act-to-act算子的计算量较大。 - 增大序列长度、批量大小、$d_{\textrm{model}}$,以及减少 head 的数量,都有助于提高算术强度。不过,序列长度和批量大小受显存限制不可能无限增加,$d_{\textrm{model}}$ 和 head 是超参数,可以看作是定值。所以,吞吐量提升的瓶颈在于显存。
增量推理
增量推理阶段,即从输出第一个 token 的过程,自回归地推理出后续的 token,直至最后一个 token 的过程。其计算和访存开销与输出的序列长度直接相关,用 $S_{out}$ 来表示其大小。对于增量推理阶段,情况比全量推理阶段要更加复杂,我们首先给出结论——对于 Decoder 的 8 个线性算子,其 FLOPS、MOPS 和算术强度如下表所示:
| Stage | FLOPS | MOPS | Arithmetic Intensity |
|---|---|---|---|
| $$Q \times W_Q$$ | $$\sum_{i=1}^{S_{out} }O(BM^2)$$ | $$\sum_{i=1}^{S_{out} }O(2BM+M^2)$$ | $$O\left(\frac{1}{\frac{2}{M}+\frac{1}{B} }\right)$$ |
| $$K \times W_K$$ | $$\sum_{i=1}^{S_{out} }O(BM^2)$$ | $$\sum_{i=1}^{S_{out} }O(2B[S_{in}+i-1]M+M^2)$$ | $$\frac{S_{out} }{\sum_{i=1}^{S_{out} }O\left( \frac{2(S_{in}+i-1)}{M} + \frac{1}{B} \right)}$$ |
| $$V \times W_V$$ | $$\sum_{i=1}^{S_{out} }O(BM^2)$$ | $$\sum_{i=1}^{S_{out} }O(2B[S_{in}+i-1]M+M^2)$$ | $$\frac{S_{out} }{\sum_{i=1}^{S_{out} }O\left( \frac{2(S_{in}+i-1)}{M} + \frac{1}{B} \right)}$$ |
| $$Q \times K$$ | $$\sum_{i=1}^{S_{out} }O(B(S_{in}+i)M)$$ | $$\sum_{i=1}^{S_{out} }O(BH[(S_{in}+i)(D+1)+D])$$ | $$\frac{S_{out} }{\sum_{i=1}^{S_{out} }O \left( \frac{1}{D} + \frac{1}{S_{in}+i} +1 \right)}$$ |
| $$P \times V$$ | $$\sum_{i=1}^{S_{out} }O(B(S_{in}+i)M)$$ | $$\sum_{i=1}^{S_{out} }O(BH[(S_{in}+i)(D+1)+D])$$ | $$\frac{S_{out} }{\sum_{i=1}^{S_{out} }O \left( \frac{1}{D} + \frac{1}{S_{in}+i} +1 \right)}$$ |
| $$A \times W_O$$ | $$\sum_{i=1}^{S_{out} }O(BM^2)$$ | $$\sum_{i=1}^{S_{out} }O(2BM+M^2)$$ | $$O\left(\frac{1}{\frac{2}{M}+\frac{1}{B} }\right)$$ |
| $$F \times W_{in}$$ | $$\sum_{i=1}^{S_{out} }O(8BM^2)$$ | $$\sum_{i=1}^{S_{out} }O(BM+4M^2)$$ | $$O\left(\frac{8}{\frac{1}{M}+\frac{4}{B} }\right)$$ |
| $$F \times W_{out}$$ | $$\sum_{i=1}^{S_{out} }O(8BM^2)$$ | $$\sum_{i=1}^{S_{out} }O(BM+4M^2)$$ | $$O\left(\frac{8}{\frac{1}{M}+\frac{4}{B} }\right)$$ |
首先注意,增量推理阶段是一个自回归的过程,因此总的 FLOPS、MOPS 和算术强度为每次推理出一个 token 的叠加,这也是表格中求和符号的由来。
其次,这里默认增量推理阶段采用 K/V Cache,因此需要 K/V Cache 的影响。K/V Cache 是一种用空间换时间的策略,因此它减少了 FLOPS,却又增加了 MOPS。具体来说,在第 $i$ 轮迭代时,已经在显存中缓存了长度为 $i-1+S_{in}$ 的 K/V 向量。此时,只需要计算当前 token 在 $W_K, W_V$ 上的投影,故此时 FLOPS 的计算复杂度与序列长度无关,即
$$ \begin{align*} O(BM^2) \end{align*} $$相应地,在第 $i$ 轮迭代时,需要从显存中读取长度为 $i-1+S_{in}$ 的 K/V 向量和计算当前 token 在 $W_K, W_V$ 上的投影所需的权重矩阵,即
$$ \begin{align*} O(2B[S_{in}+i-1]M+M^2) \end{align*} $$在后续的 MHA 计算中,第 $i$ 轮迭代的序列长度就变为 $S_{in}+i$。计算完 MHA 后,序列长度就恒为 $1$ 了,故增量推理阶段 FFN block 的相关指标与全量推理阶段相同。
通过上表,我们可以得出如下几点新的结论:
-
输入序列长度的增加直接导致 K/V Cache 线性增加,于是访存开销随之增加。这样会降低
proj的算术强度,但是却能够提升act-to-act的算术强度。 -
输出序列长度的增加直接导致自回归解码迭代次数的增加,对计算和访存的影响一定会增加。除了对 K/V 向量的
proj和act-to-act算子的 FLOPS 和 MOPS 具有二次的影响外,对其他算子的 FLOPS 和 MOPS 只是成倍增加。 -
和全量推理的情况一样,增加批量大小和 $d_{\textrm{model}}$ 和减少 head 的数量,都有助于提高算术强度。
-
输出序列长度对算术强度会有怎样的影响?下面分别就 K/V 向量的
proj和act-to-act算子的算术强度进行推导。
所以,输出序列长度的增加其实可以提高 K/V 向量 proj 的算术强度。
不过,如果要对 act-to-act 算子进行算术强度分析,涉及到如下的数列求和问题:
这相当于求调和级数的前 $S_{out}$ 项与前 $S_{in}$ 项的差。结合调和级数的前 $n$ 项和公式,得到
$$ \begin{align*} S(n) &= \sum_{i=1}^{n} \frac{1}{i} \\ \sum_{i=1}^{S_{out}} \frac{1}{i+S_{in}} &= S(S_{out}) - S(S_{in}) \\ & \approx \ln(S_{out}+1) - \ln(S_{in}+1) \\ &= \ln{\frac{S_{out}+1}{S_{in}+1}} \end{align*} $$所以,act-to-act 算子进行算术强度为
容易判断其单调性,输出序列长度的增加同样也会增加 act-to-act 算子的算术强度。
-
Vaswani, Ashish, et al. “Attention Is All You Need.” Proceedings of the 31st International Conference on Neural Information Processing Systems, Curran Associates Inc., 2017, pp. 6000–10. ↩︎
-
Devlin, Jacob, et al. “BERT: Pre-Training of Deep Bidirectional Transformers for Language Understanding.” arXiv:1810.04805 [Cs], May 2019. ↩︎
-
Radford, Alec, and Karthik Narasimhan. Improving Language Understanding by Generative Pre-Training. 2018. ↩︎
-
Touvron, Hugo, et al. LLaMA: Open and Efficient Foundation Language Models. arXiv:2302.13971, arXiv, 27 Feb. 2023. ↩︎
-
Kim, Sehoon, et al. Full Stack Optimization of Transformer Inference: A Survey. arXiv:2302.14017, arXiv, 27 Feb. 2023. ↩︎
-
本表根据 剖析 GPT 推断中的批处理效应 一文进行整理。下同。 ↩︎