线性规划问题

定义

当目标函数和约束函数都是仿射函数时，问题称为线性规划（Linear Program, LP）。线性规划问题的定义如下：

$$\begin{aligned} \mathrm{minimize} \quad & c^{\top}x+d \\ \mathrm{subject\ to} \quad & Gx \preceq h \\ \quad & Ax=b \end{aligned}$$

其中 $G \in \mathbf{R}^{m \times n}$ 并且 $A \in \mathbf{R}^{p \times n}$。显然，线性规划问题是凸优化问题。

几何意义

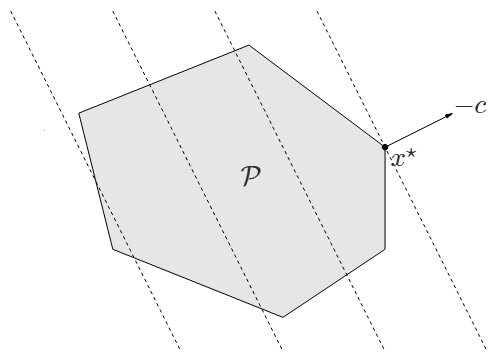
可行域 $\mathcal{P}$ 是一个多面体（图中蓝色六边形），目标函数 $c^{\top}x$ 是线性的，所以其等位曲线是与 $c$ 正交的超平面（如虚线所示）。点 $x^{\star}$ 是最优的，它是 $\mathcal{P}$ 中在方向 $-c$ 上最远的点。

线性规划的标准形式和不等式形式

在标准形式线性规划中仅有的不等式都是分量的非负约束 $x \succeq 0$

$$\begin{aligned} \mathrm{minimize} \quad & c^{\top}x \\ \mathrm{subject\ to} \quad & Ax=b \\ \quad & x \succeq 0 \end{aligned}$$

如果线性规划问题没有等式约束，则成为不等式形式线性规划

$$\begin{aligned} \mathrm{minimize} \quad & c^{\top}x \\ \mathrm{subject\ to} \quad & Ax \leqslant b \end{aligned}$$

将线性规划转化为标准形式

有时我们需要将一般的线性规划转化为标准形式。第一步是为不等式引入松弛变量 $s_i$，得到

$$\begin{aligned} \mathrm{minimize} \quad & c^{\top}x+d \\ \mathrm{subject\ to} \quad & Gx+s=h \\ \quad & Ax=b \\ \quad & s \succeq 0 \end{aligned}$$

第二步是将变量 $x$ 表示为两个非负变量 $x^+$ 和 $x^-$ 的差，即 $x=x^+-x^-$，$x^+,x^- \succeq 0$，从而得到问题

$$\begin{aligned} \mathrm{minimize} \quad & c^{\top}x^+-c^{\top}x^-+d \\ \mathrm{subject\ to} \quad & Gx^+-Gx^-+s=h \\ \quad & Ax^+-Ax^-=b \\ \quad & x^+ \succeq 0, x^- \succeq 0, s \succeq 0 \end{aligned}$$

这是标准形式的线性规划，其优化变量是 $x^+$、$x^-$ 和 $s$。

线性分式规划

在多面体上极小化仿射函数纸币的问题称为线性分式规划

$$\begin{aligned} \mathrm{minimize} \quad & \frac{c^{\top}x+d}{e^{\top}x+f} \\ \mathrm{subject\ to} \quad & Gx \preceq h \\ \quad & Ax = b \end{aligned}$$

这个函数是拟凸的（事实上是拟线性的），因此线性分式规划是一个拟凸优化问题。

转化为线性规划

如果可行集

$$\{ x \mid Gx \preceq h, Ax=b, e^{\top}x+f > 0 \}$$

非空，则线性分式规划可以转换为等价的线性规划

$$\begin{aligned} \mathrm{minimize} \quad & c^{\top}y+dz \\ \mathrm{subject\ to} \quad & Gy-hz \preceq 0 \\ \quad & Ay-bz=0 \\ \quad & e^{\top}y + fz = 1 \\ \quad & z \geqslant 0 \end{aligned}$$

其优化变量为 $y$ 和 $z$。